高校数学の「数1」公式一覧とそれぞれ公式の証明をまとめました.大学受験などにご活用いただけたら幸いです.すでに高校を卒業した方でも,パズル感覚で公式の証明をするのも楽しいので,ぜひチャレンジしてみてください.
各公式の右下にその公式の証明のリンクがあります。
数と式
二重根号
二重根号 \(・\sqrt{a+b+2\sqrt{ab}}=\sqrt{a}+\sqrt{b} \)
\(・\sqrt{a+b-2\sqrt{ab}}=\sqrt{a}-\sqrt{b}\) (a>bのとき)
集合と論理
集合のド・モルガンの法則
集合のド・モルガンの法則 \(・\overline{A∪B}=\overline{A}∩\overline{B}\)
\(・\overline{A∩B}=\overline{A}∪\overline{B}\)
二次関数
二次方程式の解の公式
二次方程式の解の公式 2次方程式ax2+bx+c=0の解は
$$x=\frac{-b±\sqrt{b^{2}-4ac}}{2a}$$
図形と計量
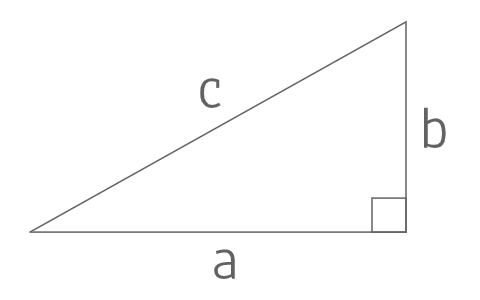
三平方の定理
三平方の定理$$c^2=a^2+b^2$$
三角比の相互関係
三角比の相互関係 \(・sin^{2}θ+cos^{2}θ=1\)
\( ・tanθ=\frac{sinθ}{cosθ}\)
\(・1+tan^{2}θ=\frac{1}{cos^{2}}\)
90°-θの三角比
90°-θの三角比 \(・sin(90°-θ)=cosθ\)
\(・cos(90°-θ)=sinθ\)
\(・tan(90°-θ)=\frac{1}{tanθ}\)
180°-θの三角比
180°-θの三角比 \(・sin(180°-θ)=sinθ\)
\(・cos(180°-θ)=-cosθ\)
\(・tan(180°-θ)=-tanθ \)
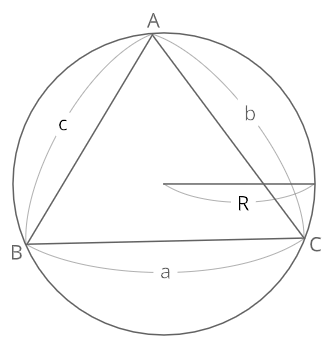
正弦定理
正弦定理 \(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R\)
(Rは△ABCの外接円の半径)
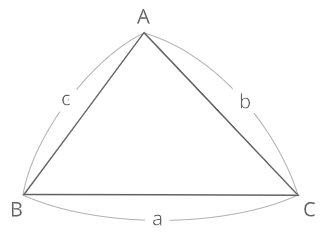
余弦定理
余弦定理\(・a^{2}=b^{2}+c^{2}-2bccosA\)
\(・b^{2}=c^{2}+a^{2}-2cacosB\)
\(・c^{2}=a^{2}+b^{2}-2abcosC\)
データの分析
分散と標準偏差
分散と標準偏差・分散
\(s^{2}=\frac{1}{n}\{(x_1-\overline{x})^2+(x_2-\overline{x})^2+・・・+(x_n-\overline{x})^2\}\)
・標準偏差
\(s=\sqrt{\frac{1}{n}\{(x_1-\overline{x})^2+(x_2-\overline{x})^2+・・・+(x_n-\overline{x})^2\}}\)


