“集合のド・モルガンの法則”の公式とその証明です!
集合のド・モルガンの法則
公式
集合のド・モルガンの法則 \(・\overline{A∪B}=\overline{A}∩\overline{B}\)
\(・\overline{A∩B}=\overline{A}∪\overline{B}\)
証明
べん図による\(\overline{A∪B}=\overline{A}∩\overline{B}\)の証明
証明
\(\overline{A∪B} \)
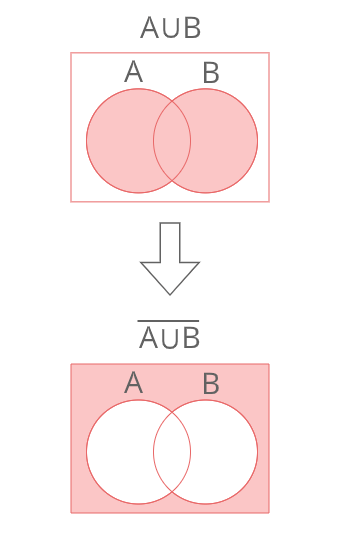
\(\overline{A}∩\overline{B}\)
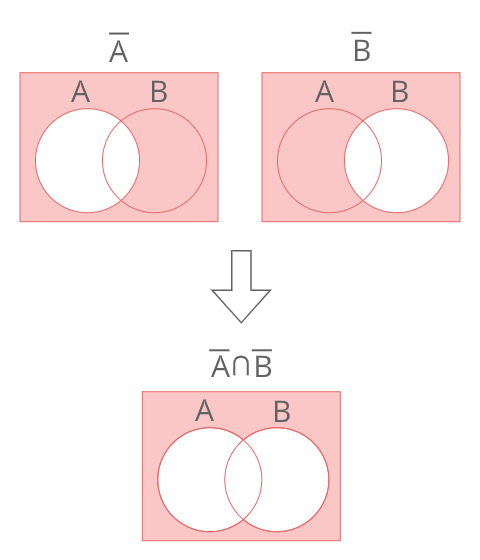
左辺と右辺をそれぞれ上のようにべん図で表すと、両辺で等しくなる。
よって
\(\overline{A∪B}=\overline{A}∩\overline{B}\)
べん図による\(\overline{A∩B}=\overline{A}∪\overline{B}\)の証明
証明
\(\overline{A∩B}\)
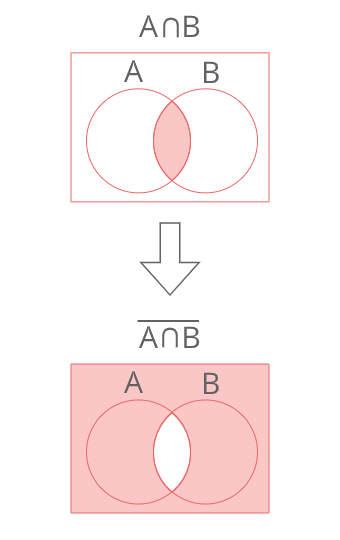
\(\overline{A}∪\overline{B}\)
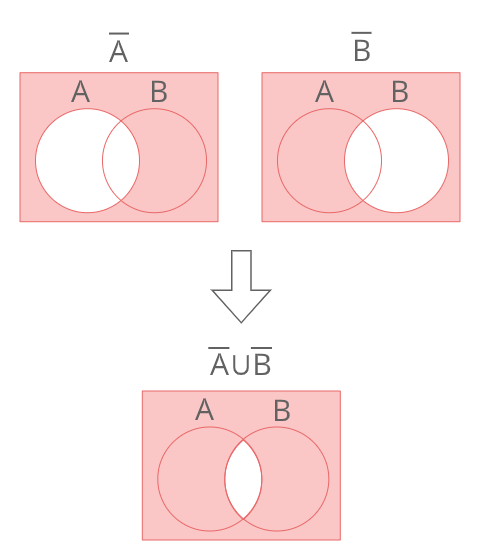
左辺と右辺をそれぞれ上のようにべん図で表すと、両辺で等しくなる。
よって
\(\overline{A∩B}=\overline{A}∪\overline{B}\)
問題
Q
要素全体が{1, 2, 3, 4, 5, 6, 7, 8}, \(A\)={1, 2, 3, 4} , \(B\)={3, 4, 5, 6}のとき,\(\overline{A\cup B}\)の要素を示せ.
A
\(A\cup B\)={1, 2, 3, 4, 5, 6}であるため
\(\overline{A\cup B}\)={7, 8}
A(別解)
ド・モルガンの法則のより
\(\overline{A\cup B}=\overline{A}\cap\overline{B}\) ①
\(\overline{A}\)={3, 4, 5, 6, 7, 8}
\(\overline{B}\)={1, 2, 7, 8}
\(\overline{A}\cap \overline{B}\)={7, 8} ②
①, ②より
\(\overline{A\cup B}\)={7, 8}
まとめ
上に示した問題ではド・モルガンの法則は大して必要がないようにも思えますが,複雑な場合はよりシンプルにすることができます.電気系の工学部では論理回路でよく使われます.



