“正弦定理”の公式とその証明です！
正弦定理
公式
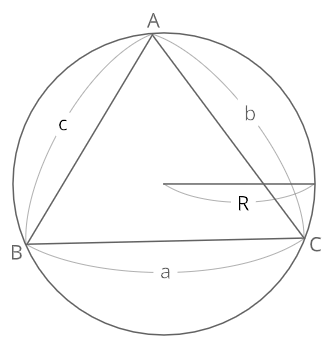
正弦定理 \(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R\)
(Rは△ABCの外接円の半径)
証明
以下で\(\frac{a}{sinA}=2R\)について∠Ａが鋭角、直角、鈍角のときに分けて証明します。また∠Ｂ、∠Ｃにおいても同様に証明できます。
鋭角(∠A<90°)のとき
証明 
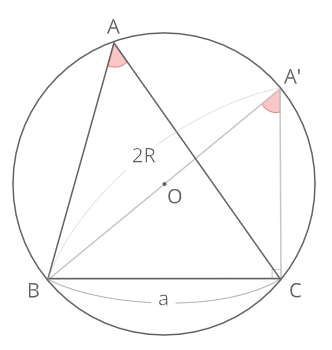
1辺が円の中心Ｏを通るようにＡをＡ’に移動させると、∠A’CB=90°となるため
\(2RsinA’=a\)
円周角の定理より∠Ａ=∠A’となるため
\(2RsinA=a\)
よって
\(\frac{a}{sinA}=2R\)
すなわち
\(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R\)
直角(∠A=90°)のとき
証明 
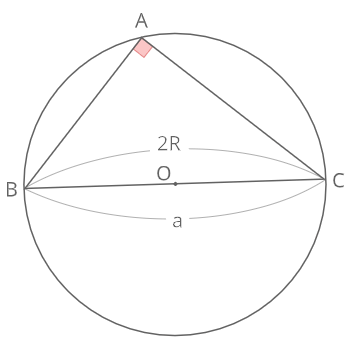
\(sinA=sin90°=1\)
∠Ａ=90°でありBCは円の中心を通るため
\(2R=a=\frac{a}{1}=\frac{a}{sin90°}=\frac{a}{sinA}\)
よって
\(\frac{a}{sinA}=2R\)
すなわち
\(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R\)
鈍角(∠A>90°)のとき
証明 
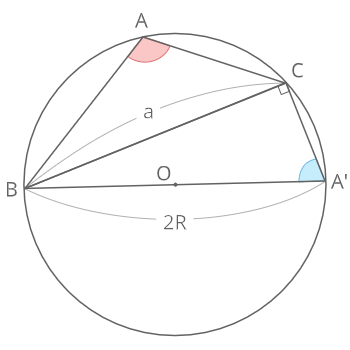
BA’が円の中心を通るようにA’をとると、四角形ABA’Cは円に内接するため円に内接する四角形より
\(∠A’=180°-∠A\)
また∠BCA’=90°であるため
\(a=2RsinA’\)
180°-θの三角比より
\(=2Rsin(180°-A)=2RsinA\)
よって
\(\frac{a}{sinA}=2R\)
すなわち
\(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R\)
問題
Q
円Oに内接する三角形が図のようなとき，円Oの半径Rを求めよ
A
正弦定理より
\(2R=\frac{2}{sin60°}\)
\(=\frac{2}{\frac{\sqrt{3}}{2}}\)
\(=\frac{4}{\sqrt{3}}\)
\(=\frac{4\sqrt{3}}{3}\)
⇒\(R=\frac{2\sqrt{3}}{3}\)
となります．
まとめ
正弦定理は円と内接する円の関係を表す式です．図形の問題で実は正弦定理が使えたのにということもよくあるので常に頭の片隅に置いておくといいと思います．
