“180°-θの三角比”の公式とその証明です!
180°-θの三角比
公式
180°-θの三角比 \(・sin(180°-θ)=sinθ\)
\(・cos(180°-θ)=-cosθ\)
\(・tan(180°-θ)=-tanθ \)
証明
図形による証明
証明
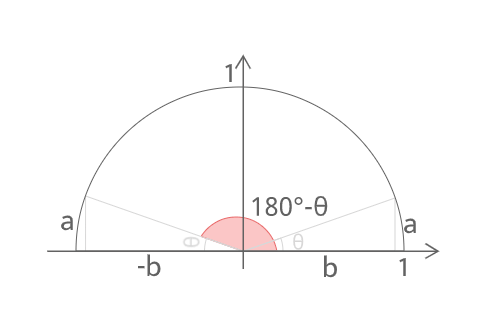
上の図より
\(・sinθ=a\)
\(・cosθ=b\)
\(・tanθ=\frac{a}{b}\)
また
\(・sin(180°-θ)=a\)
\(・cos(180°-θ)=-b\)
\(・tan(180°-θ)=-\frac{a}{b}\)
以上より
\(・sin(180°-θ)=a=sinθ\)
\(・cos(180°-θ)=-b=-cosθ\)
\(・tan(180°-θ)=-\frac{a}{b}=-tanθ\)
よって
\(・sin(180°-θ)=sinθ\)
\(・cos(180°-θ)=-cosθ\)
\(・tan(180°-θ)=-tanθ \)
問題
Q
\(tan(180°-\theta)\)を\(cos\theta\), \(sin\theta\)で表せ
A
180°-θの三角比, 三角関数の相互関係より
\(tan(180°-\theta)\)
\(=-\tan\theta\)
\(=-\frac{sin\theta}{cos\theta}\)
まとめ
180°-θの三角比を覚えるよりは頭の中で図を思い浮かべて導き出せると便利です.



