高校数学の「数2」公式一覧とそれぞれ公式の証明をまとめました.大学受験などにご活用いただけたら幸いです.すでに高校を卒業した方でも,パズル感覚で公式の証明をするのも楽しいので,ぜひチャレンジしてみてください.
各公式の右下にその公式の証明のリンクがあります。
方程式・式と証明
二項定理
二項定理 \((a+b)^n=_nC_0a^n+_nC_1a^{n-1}b+…_nC_ra^{n-r}b^r+\)
\(…_nC_{n-1}ab^{n-1}+_nC_nb^n\)
\( =\displaystyle \sum_{k=0}^n {}_nC_k a^{n-k}b^k \)
相加平均と相乗平均
相加平均と相乗平均a≧0、b≧0のとき
\(\frac{a+b}{2}≧\sqrt{ab}\)
図形と方程式
内分点・外分点の座標
内分点・外分点の座標2点\(A(x_1, y_1), B(x_2, y_2)\)を結ぶABがあるとき
・m:n に内分する点の座標は
\((\frac{nx_1+mx_2}{m+n}, \frac{ny_1+my_2}{m+n})\)
・m:n に外分する点の座標は
\((\frac{-nx_1+mx_2}{m-n}, \frac{-ny_1+my_2}{m-n})\)
三角形の重心
三角形の重心
\(A(x_1, y_2), B(x_2, y_2), C(x_3, y_3)\)からなる△ABCの重心の座標は
\((\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3})\)
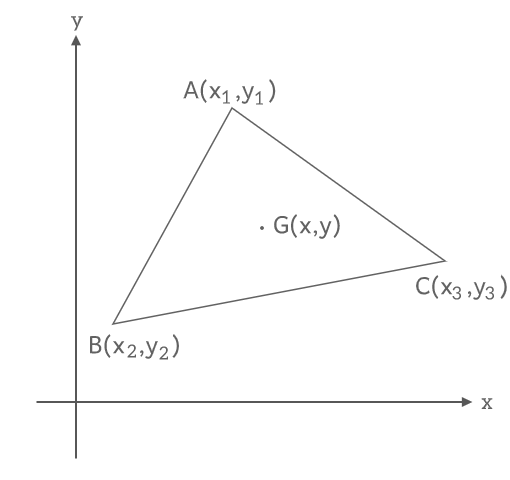
点と直線の距離
点と直線の距離点\((x_1, y_1)\)と直線ax+by+c=0の距離dは
\(d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
円の方程式
円の方程式(a, b)を中心とする半径rの円の方程式は
\((x-a)^2+(y-b)^2=r^2\)
三角関数
扇形の弧の長さと面積
扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると
\(・l=rθ\)
\(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)
三角関数の相互関係
三角関数の相互関係 \(・sin^2θ+cos^2θ=1\)
\(・tanθ=\frac{sinθ}{cosθ}\)
\(・1+tan^2θ=\frac{1}{cos^2θ}\)
加法定理
加法定理\(・sin(α+β)=sinαcosβ+cosαsinβ\)
\(・sin(α-β)=sinαcosβ-cosαsinβ\)
\(・cos(α+β)=cosαcosβ-sinαsinβ\)
\(・cos(α-β)=cosαcosβ+sinαsinβ\)
\(・tan(α+β)=\frac{tanα+tanβ}{1-tanαtanβ}\)
\(・tan(α-β)=\frac{tanα-tanβ}{1+tanαtanβ}\)
2倍角の公式
2倍角の公式\(・sin2α=2sinαcosα\)
\(・cis2α=cos^2α-sin^2α\)
\(=1-2sin^2α=2cos^2α-1\)
\(・tan2α=\frac{2tanα}{1-tan^2α}\)
半角の公式
半角の公式 \(・sin^2\frac{α}{2}=\frac{1-cosα}{2}\)
\(・cos^2\frac{α}{2}=\frac{1+cosα}{2}\)
三角関数の合成
三角関数の合成$$asinθ+bcosθ=\sqrt{a^2+b^2}sin(θ+α)$$
積和の公式
積和の公式\(・sinαcosβ=\frac{1}{2}(sin(α+β)+sin(α-β))\)
\(・cosαsinβ=\frac{1}{2}(sin(α+β)-sin(α-β))\)
\(・cosαcosβ=\frac{1}{2}(cos(α+β)+cos(α-β))\)
\(・sinαsinβ=-\frac{1}{2}(cos(α+β)-cos(α-β))\)
和積の公式
和積の公式 \(・sinα+sinβ=2sin\frac{α+β}{2}cos\frac{α-β}{2}\)
\(・sinα-sinβ=2cos\frac{α+β}{2}sin\frac{α-β}{2}\)
\(・cosα+cosβ=2cos\frac{α+β}{2}cos\frac{α-β}{2}\)
\(・cosα-cosβ=-2sin\frac{α+β}{2}sin\frac{α-β}{2}\)
指数関数・対数関数
対数と指数
対数と指数a≠1、a>0、M>0のとき
\(log_aM=p ⇔ a^p=M\)
対数の性質
対数の性質 a≠1、a>0、M>0、N>0のとき
\(・log_a1=0\)
\(・log_aa=1\)
\(・log_aMN=log_aM+log_aN\)
\(・log_a\frac{M}{N}=log_aM-log_aN\)
\(・log_aM^r=rlog_aM\)
底の変換公式
底の変換公式a≠1、c≠1でa、b、cが正の数のとき
\(log_ab=\frac{log_cb}{log_ca}\)
微分と積分
導関数の定義
導関数の定義$$f'(x)=\lim_{h→0}\frac{f(x+h)-f(x)}{h}$$
xⁿの導関数
xⁿの導関数xが自然数のとき
\((x^n)’=nx^{n-1}\)
定積分
定積分$$\int_a^bf(x)dx=[F(x)]_a^b=F(b)-F(a)$$


