“三角形の重心”の公式とその証明です!
三角形の重心
公式
三角形の重心
\(A(x_1, y_2), B(x_2, y_2), C(x_3, y_3)\)からなる△ABCの重心の座標は
\((\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3})\)
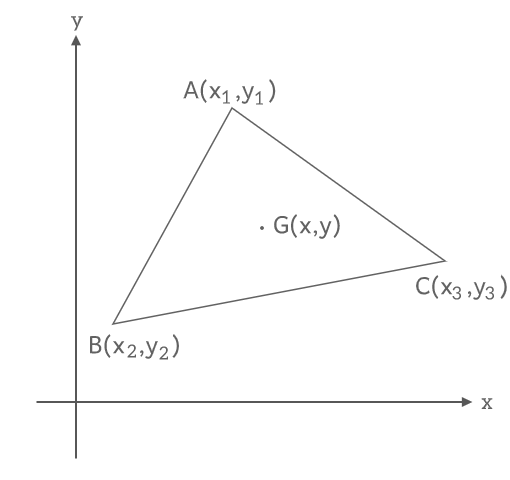
証明
内分点の座標による証明
証明
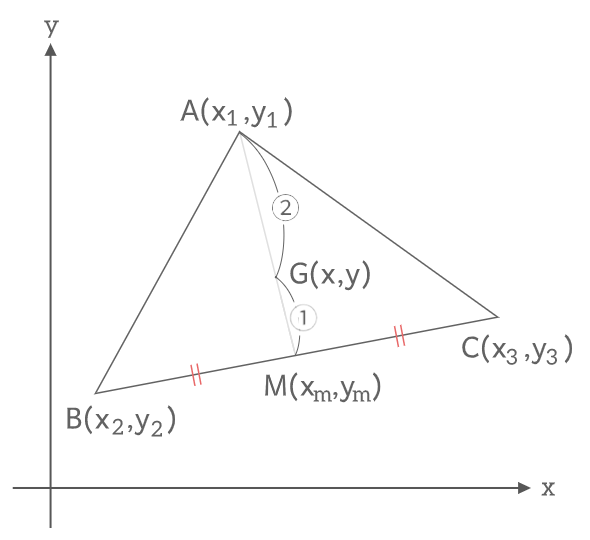
BCの中点を\(M(x_m,y_m)\)とすると
内分点の座標より
\(M(x_m,y_m)=M(\frac{x_2+x_3}{2} , \frac{y_2+y_3}{2})\)
重心G(x,y)は重心の性質より
\(AG:GM=2:1\)
また内分点の座標より
\(x=\frac{x_1+2x_m}{2+1}\)
\(=\frac{x_1+2×\frac{x_2+x_3}{2}}{3}=\frac{x_1+x_2+x_3}{3}\)
\(y=\frac{y_1+2y_m}{2+1}\)
\(=\frac{y_1+2×\frac{y_2+y_3}{2}}{3}=\frac{y_1+y_2+y_3}{3}\)
よって
\(A(x_1, y_2), B(x_2, y_2), C(x_3, y_3)\)からなる△ABCの重心の座標は
\((\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3})\)



