“内分点・外分点の座標”の公式とその証明です!
内分点・外分点の座標
公式
内分点・外分点の座標2点\(A(x_1, y_1), B(x_2, y_2)\)を結ぶABがあるとき
・m:n に内分する点の座標は
\((\frac{nx_1+mx_2}{m+n}, \frac{ny_1+my_2}{m+n})\)
・m:n に外分する点の座標は
\((\frac{-nx_1+mx_2}{m-n}, \frac{-ny_1+my_2}{m-n})\)
証明
内分点の座標の証明
証明
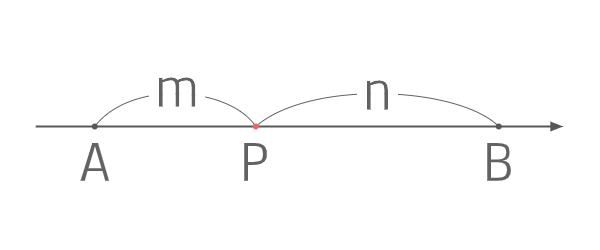
まず一次元について解く
それぞれの座標を\(A(a) , B(b) , P(p)\)とすると
\(\vec{AP}:\vec{PB}=p-a:b-p=m:n\)
⇒ \(m(b-p)=n(p-a)\)
⇒ \(p=\frac{na+mb}{m+n}\)
二次元のときもx座標とy座標をそれぞれ同様に導き出せる。
よって
m:n に内分する点の座標は
\((\frac{nx_1+mx_2}{m+n}, \frac{ny_1+my_2}{m+n})\)
外分点の座標の証明
証明
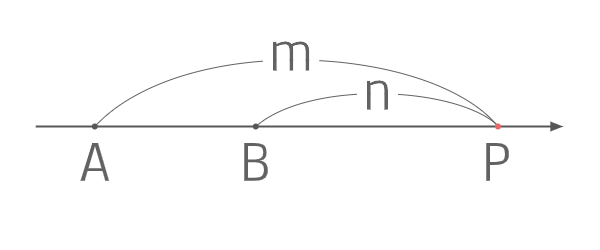
まず一次元について解く
それぞれの座標を\(A(a) , B(b) , P(p)\)とすると
\(\vec{AP}:\vec{PB}=p-a:-(b-p)=m:n\)
⇒ \(m(-b+p)=n(p-a)\)
⇒ \(p=\frac{-na+mb}{m-n}\)
二次元のときもx座標とy座標をそれぞれ同様に導き出せる。
よって
m:n に外分する点の座標は
\((\frac{-nx_1+mx_2}{m-n}, \frac{-ny_1+my_2}{m-n})\)



