高校物理の電磁気①の定義・法則などをまとめました。勉強に役立ててもらえれば幸いです。
電荷
電磁気学とは

電磁気とは、電気と磁気の性質やその相互作用を研究する学問です。この分野では、電荷、電場、磁場、電流といった基本的な概念を学びます。電気は電荷の移動によって生じ、磁気は電流や磁石によって生じます。この2つが互いに影響し合うことを研究するのが電磁気学です。
電磁気学は日常生活で大きな役割を果たしています。例えば、スマートフォンやコンピュータ、テレビなどの電子機器はすべて電磁気の原理を利用しています。電力を送る電線や電気モーター、発電機も電磁気の応用です。また、医療分野では、MRI(磁気共鳴画像装置)が体の内部を詳しく見るために使われています。電磁気の原理は、現代社会の多くの便利なものを支えている重要な学問です。
原子
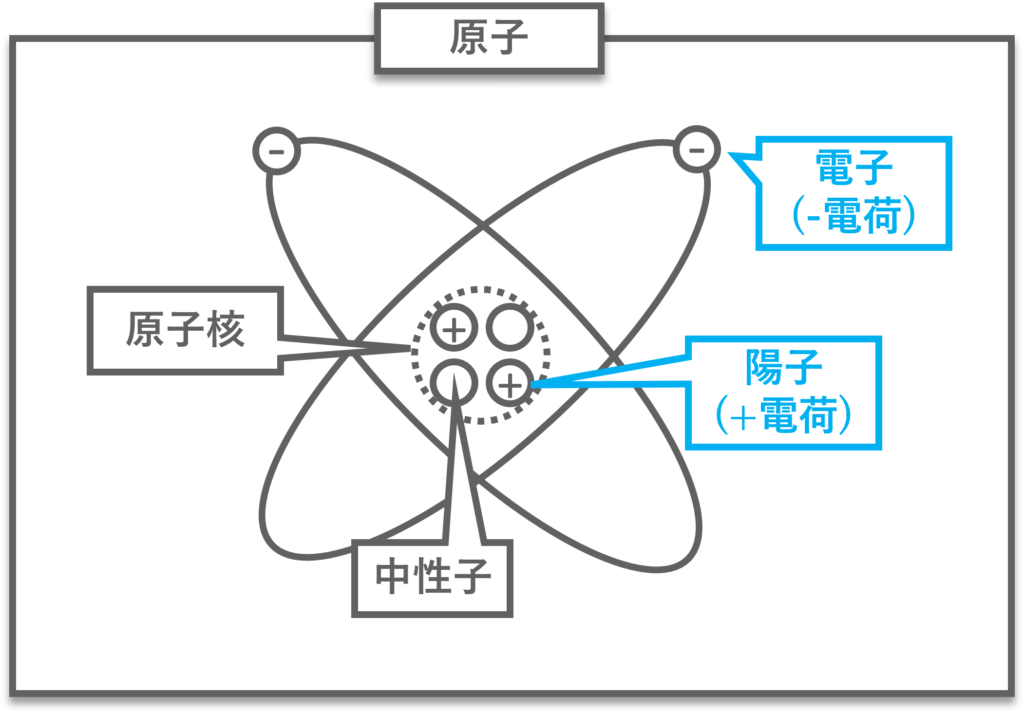
・原子 (atom):すべての物質の基本粒子
・原子核 (nucleus):原子の構成要素の一つで,原子の中心部
・陽子 (proton):原子核の構成要素の一つで,+ (プラス)の電荷を持つ
・中性子 (neutron):原子核の構成要素の一つで,電荷を持たない
・電子 (electron):原子の構成要素の一つで,- (マイナス)の電荷を持つ
・電荷 (electric charge):電気の量.電気現象のもとなる.
イオン
通常の原子は陽子の数と電子の数が同じで,+と-の電荷が打ち消しあって原子としては電荷を持たない状態にある.
イオン (Ion)は原子から1つ以上の電子がいなくなった状態か,1つ以上の電子を過剰にもっている原子のことである.例えば1つの電子を失ったイオンは1荷の陽イオン,1つの電子が付加されたイオンを1荷の陰イオンという.
電荷・素電荷 (電気素量)
電荷 (electric charge)は電子と陽子のように,電気的な作用を及ぼす源のことである.
素電荷 (電気素量)は電荷の最小単位であり,電子と陽子が素電荷である.電子と陽子の電荷量は等しく,値は以下の通りである.
$$e≒1.60\times 10^{-19} \mathtt{[C]}$$
単位 [C]:クーロン (coulomb).電荷の量を表す単位.
クーロンの法則
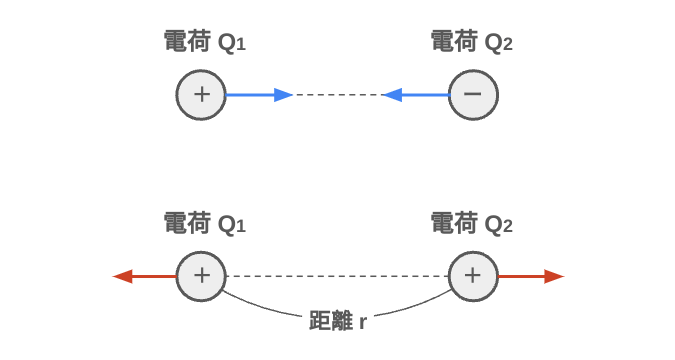
真空中に2つの電荷\(Q_1\),\(Q_2\)が距離\(r\)離れて位置するとき,各電荷には以下の力 (クーロン力)が働く.\(Q_1,Q_2\)が同符号のときは反発力,\(Q_1,Q_2\)が異符号のときは吸引力であることを示す.
$$F=k\frac{Q_1Q_2}{r^2} \mathtt{[N]}$$
- \(k=\frac{1}{4\pi \epsilon_0}\)
- \(\epsilon_0=\frac{10^7}{4\pi c}\approx 8.85\times 10^{-12}\)[F/m]:真空の誘電率 (電荷と電荷によって働く力の関係を示す係数)
- 単位 [F]:ファラド (farad).静電容量の単位
- \(c\):高速
重ね合わせの原理
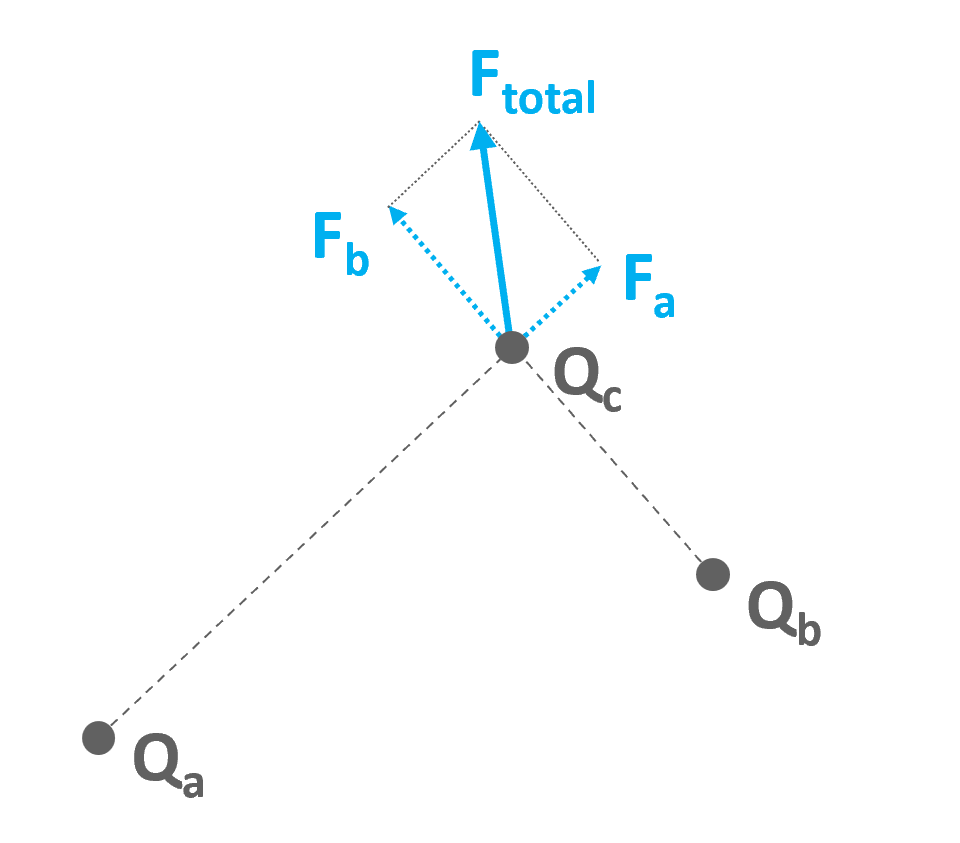
任意の2つの電荷に働くクーロン力は他の電界によって変化しない.複数の電荷がある場合は,それぞれのクーロン力のベクトルを合成したクーロン力が働く.これを重ね合わせの原理 (Principle of Superposition)という.
静電誘導
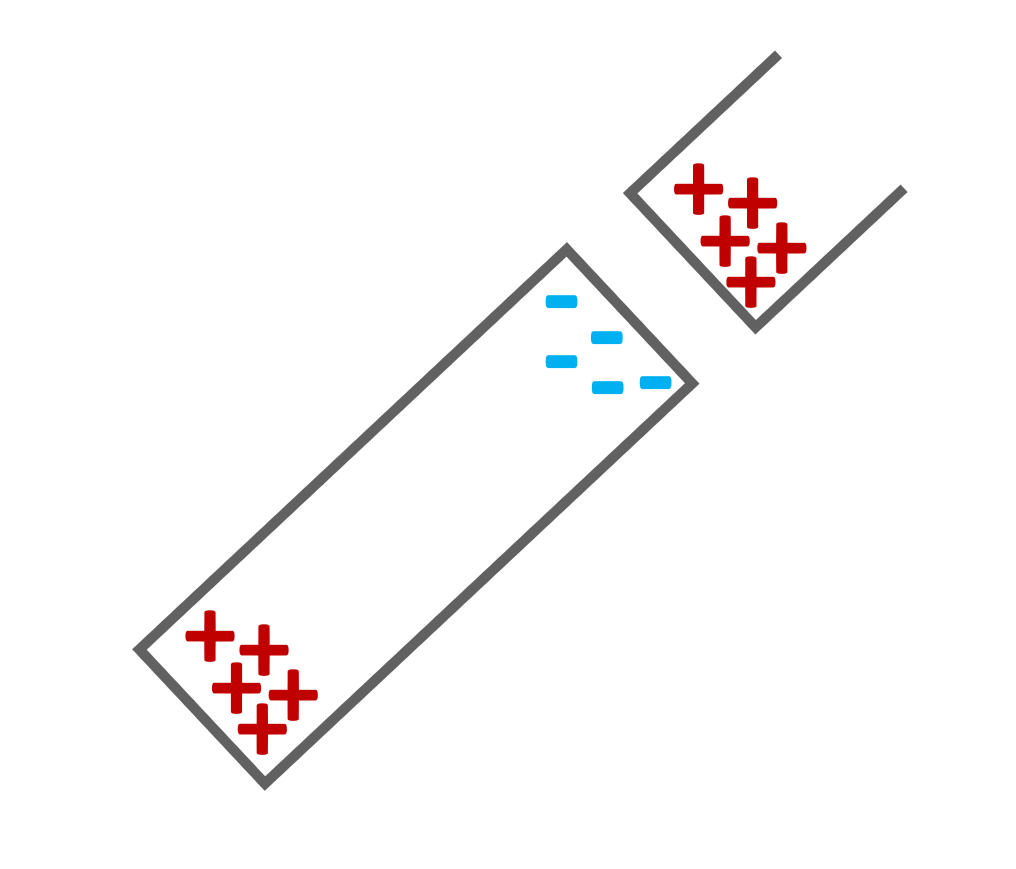
帯電した導体 (金属など)を他の導体に近づけると,帯電した電荷と異符号の電荷が近くに誘導され,同符号の電荷は遠くへと誘導させる.この現象を静電誘導 (electrostatic induction)という.
電荷の保存則
複数の電荷が移動しても電荷の総量は保存される.
(電荷の生成・消滅,素粒子の崩壊が起こるまで)
電界・静電界
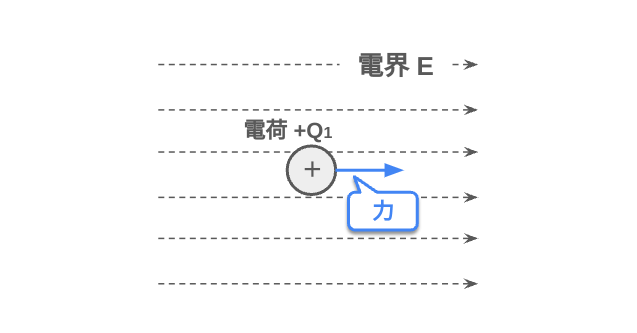
電荷はその周りに電気的な場 (界)をつくり,他の電荷に電気的な力を作用させる.この電気的な場を電界 (電場)を呼ぶ.特に電荷が静止している場を静電界と呼ぶ.
電界\(\vec{E}\)がかかる位置にある電荷\(q\)には,以下の力\(\vec{F}\)が働く.
$$\vec{F}=q\vec{E} \mathtt{[N/C]}$$
・単位 [C]:クーロン (coulomb).電荷の量を表す単位.
・電界の単位:[N/C]=[N・m/C・m]=[J/C・m]=[V/m]
点電荷からの電界
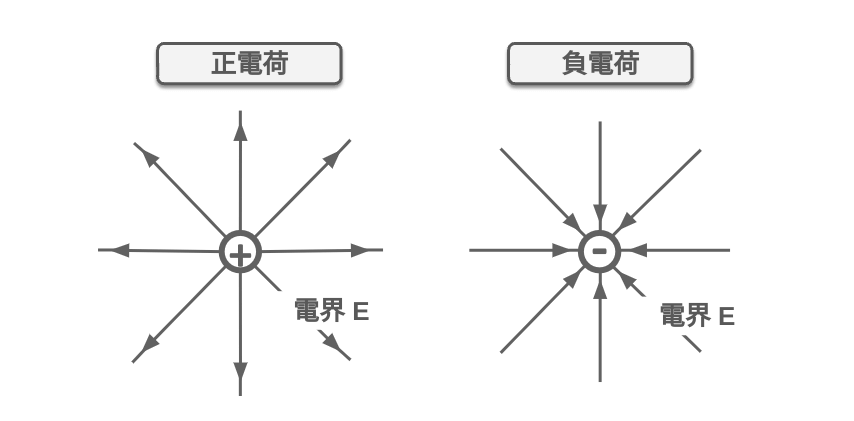
真空中のある点電荷\(Q [C]\)から\(r [m]\)離れた点にかかる電界\(E\)は以下である.
$$E=\frac{Q}{4\pi \epsilon_0 r^2} \mathtt{[N/C]}$$
・\(\epsilon_0=\frac{10^7}{4\pi c}\approx 8.85\times 10^{-12}\)[F/m]:真空の誘電率 (電荷と電荷によって働く力の関係を示す係数)
・\(c\):高速
電気力線
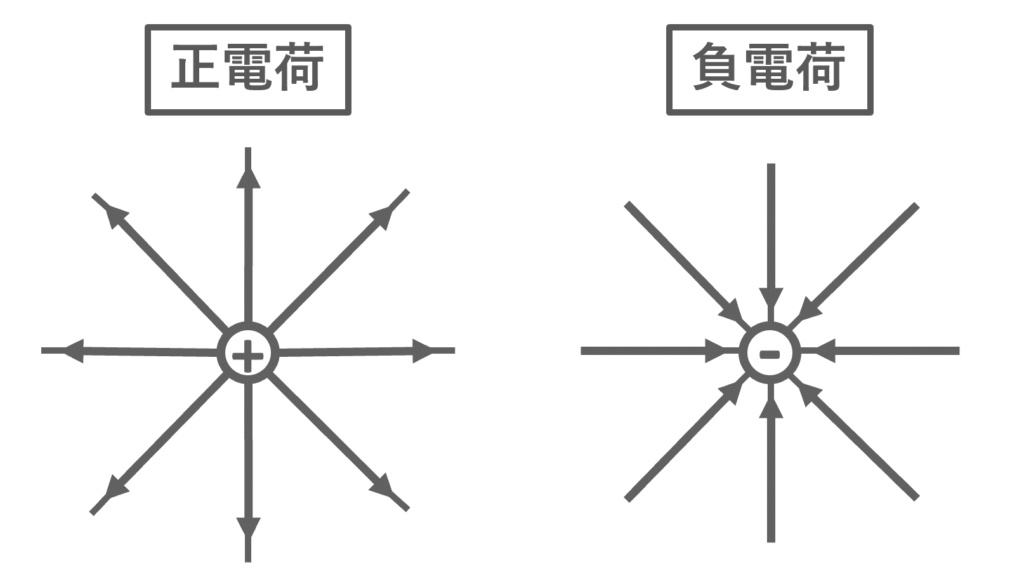
電気力線 (Electric line of force)は電界を示す仮想的な線である.以下の性質を持つ.
① 電気力線は正電荷から始まり,負電荷に終わる
② 電気力線の向きは電界の向きを表す
③電気力線の密度は電界の大きさを表す
電位・電位差 (電圧)
電位 (potential)は電荷\(Q\)にかかる電気的な位置エネルギーのことで,単位は[V (ボルト)]=[J/C]である.この位置エネルギーは無限に遠いところを基準としているが,実用上では地球 (アース)を基準にする.
また,無限遠や地球以外のある点の電位を基準としたときの,ある点での電位との差を電位差 (電圧 (voltage))という.
真空中のある点電荷\(Q\)から距離\(r\)離れた点の電位は以下の通りである.
$$V=\frac{Q}{4\pi \epsilon_0 r} \mathtt{[V]}$$
・電位の単位:[V (ボルト)]
・\(\epsilon_0=\frac{10^7}{4\pi c}\approx 8.85\times 10^{-12}\)[F/m]:真空の誘電率 (電荷と電荷によって働く力の関係を示す係数)
・\(c\):高速
電位の傾きと電界
電位\(V\),距離\(r\),電界\(E\)とすると,電位の傾きと電界は以下の関係がある.
$$\frac{dV}{dr}=-E \mathtt{[V/m]}$$
電界の単位:[N/C]=[N・m/C・m]=[J/C・m]=[V/m]
ガウスの法則
真空中にある電荷\(Q\)の周りで閉じるように (閉曲面)電界と微小面積を積分した値 (面積分)は以下の関係を持つ.
$$\oint_SE_ndS=\frac{Q}{\epsilon_0}$$
これを電界に関するガウスの法則 (ガウスの法則,Gauss’ law)という.これは電荷\(Q\)から出ていく電気力線の数ははどのような閉曲面をとっても等しいことを示す.
導体・誘電体
導体とは
導体は金属などの電気を通しやすい物体のこと.
静電しゃへい
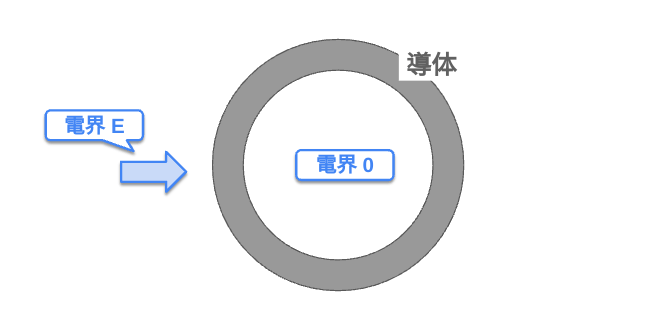
導体で作られた空間内では,外部の電界を遮る.これを静電しゃへい (シールド)という.
電界内にある導体は静電誘導によって外部との電界を打ち消しあうため,導体内では外部の電界の影響を受けないためである.
測定器などで外部の電界を影響を抑えることに用いられる.
誘電体 (絶縁体)とは
誘電体は導体と比較して,誘電しやすい物質のことです.また電気を通しにくい性質から絶縁体ともいわれます.
分極
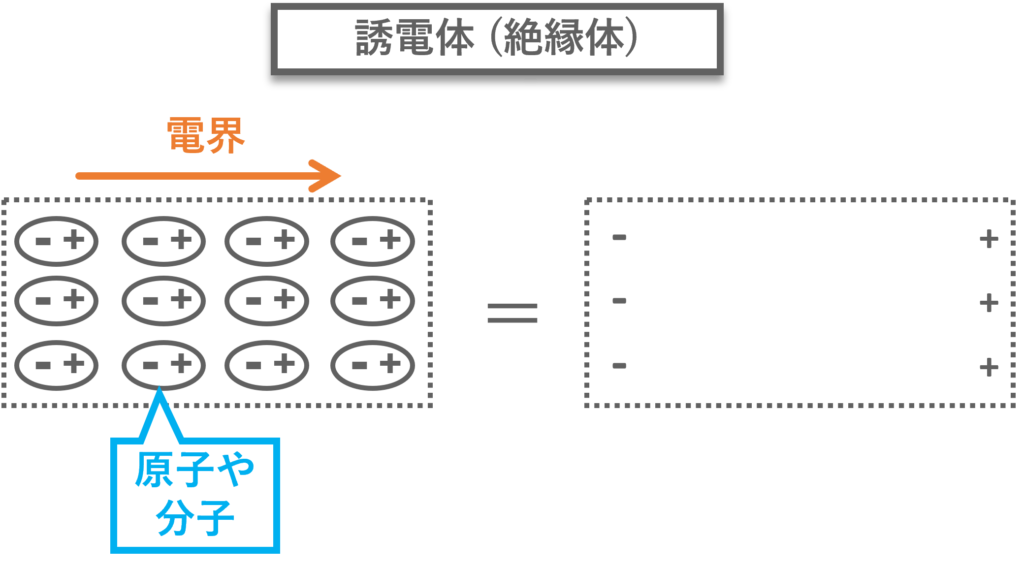
分極とは、物質の内部で正の電荷と負の電荷が分かれて配置される現象です。電場が加わると電子が反対方向に移動して正負の電荷が分かれます。
分極は、コンデンサーなどの電子部品や液晶ディスプレイの技術に利用されています。コンデンサーでは、分極によって電荷を蓄えることができ、電気回路の中でエネルギーを一時的に保存する役割を果たします。
コンデンサ
コンデンサ
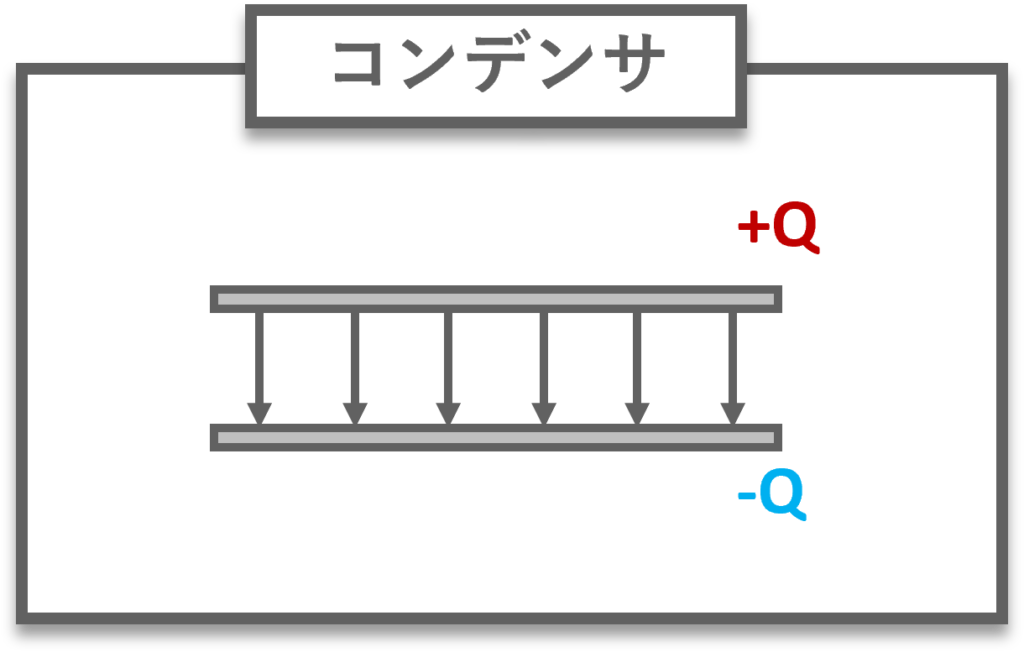
2つの導体にそれぞれ電荷+Qと電荷-Qを与えて近づけると,電気力線は一つからもう一つへと終端される.このように電荷を蓄えることができる素子をコンデンサ (蓄電器,キャパシタ (capacitor))という.
静電容量

2つの導体にそれぞれ電荷+Qと電荷-Qを与え,2つの導体の電位差がVのとき,\(Q=CV\)が成り立つ.Cは静電容量 (キャパシタンス (capacitance))といい,単位はF (ファラド (farad))である.静電容量は電荷をどれだけ蓄えられるかを示す.
比誘電率
導体と導体の間が真空の時の静電容量を\(C_0\),導体間に誘電体がある場合の静電容量を\(C\)とすると,以下の関係があります.\(\epsilon_r\)は比誘電率と呼ばれ,誘電体の材料によってきまります.誘電体は比誘電率が\(\epsilon_r\)が高く,比誘電率が高いと同じ電荷量に対して,導体間の電圧と電界が\(\frac{1}{\epsilon_r}\)倍に小さくなります.
$$\frac{C}{C_0}=\epsilon_r$$
平行導体板の静電容量
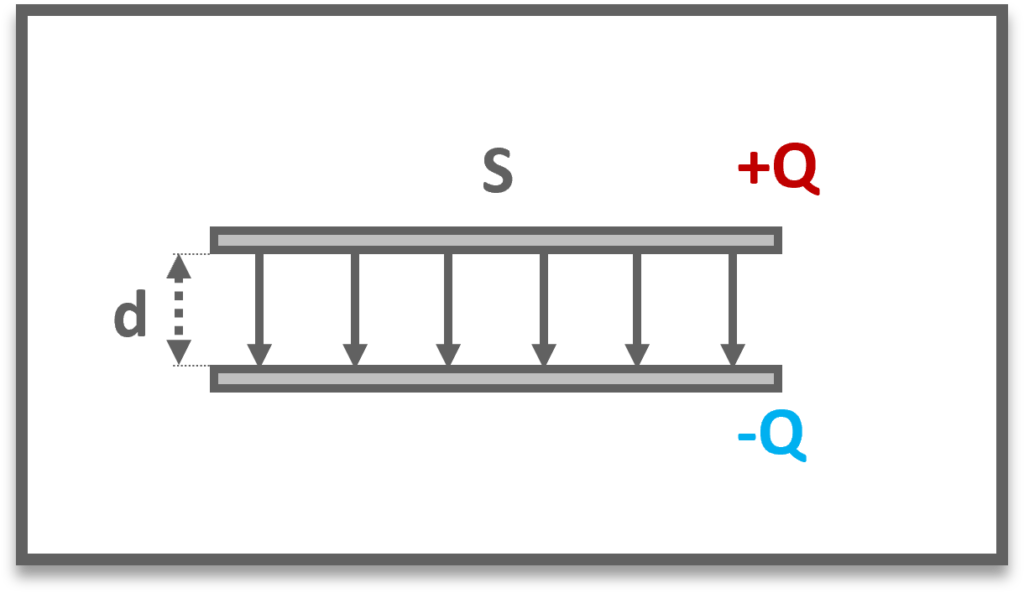
平行導体板の静電容量は以下の通りである.
$$C=\frac{Q}{V}=\frac{\epsilon_0S}{d}$$
コンデンサの並列接続
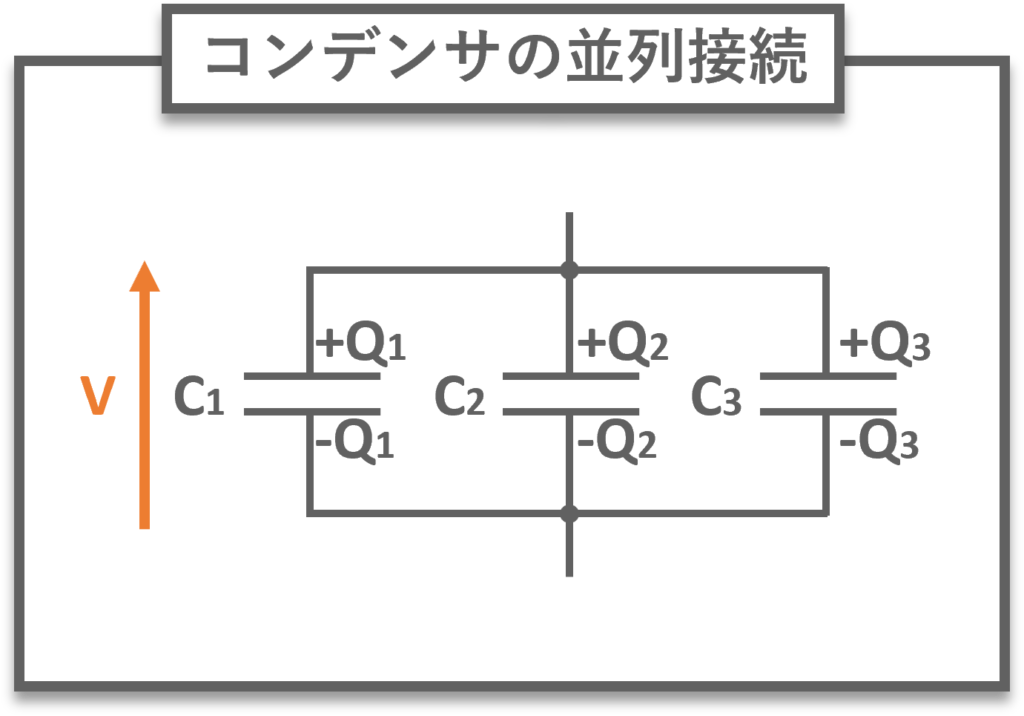
コンデンサの並列接続の合成容量\(C_{合成}\)は以下のようになります.
\(Q_1=C_1V,\)
\(Q_2=C_2V,\)
\(Q_3=C_3V,\)
\(Q_{合成}=Q_1+Q_2+Q_3\)より
\(C_{合成}=\frac{Q_{合成}}{V}\)
\( =C_1+C_2+C_3\)
コンデンサの直列接続

コンデンサの直列接続の合成容量\(C_{合成}\)は以下のようになります.
\(V_1=\frac{Q}{C_1},\)
\(V_2=\frac{Q}{C_2},\)
\(V_3=\frac{Q}{C_3}\)
⇒\(V=V_1+V_2+V_3\)
⇒\(C_{合成}=\frac{Q}{V}\)
⇒\(\frac{1}{C_{合成}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\)
コンデンサのエネルギー
コンデンサのエネルギーは以下の通りです.
$$W=\frac{1}{2}\frac{Q^2}{C}=\frac{1}{2}QV=\frac{1}{2}CV^2 [J]$$
まとめ
本記事では高校物理の「電磁気学」の定義や法則の①をまとめました。
電磁気学は日常生活で大きな役割を果たしています。例えば、スマートフォンやコンピュータ、テレビなどの電子機器はすべて電磁気の原理を利用しています。電力を送る電線や電気モーター、発電機も電磁気の応用です。電磁気の原理は、現代社会の多くの便利なものを支えている重要な学問です。
本記事で少しでも高校物理の「電磁気学」の学習に役立てていたら幸いです。
その他の高校物理まとめは下記の黄色い枠のリンクから↓



