高校数学の「数A」公式一覧とそれぞれ公式の証明をまとめました.大学受験などにご活用いただけたら幸いです.すでに高校を卒業した方でも,パズル感覚で公式の証明をするのも楽しいので,ぜひチャレンジしてみてください.
各公式の右下にその公式の証明のリンクがあります。
場合の数と確率
和集合・補集合
和集合・補集合\(・n(A∪B)=n(A)+n(B)-n(A∩B)\)
\(・n(\overline{A})=n(U)-n(A)\)
順列
順列$$_nP_r=n(n-1)(n-2)・・・(n-r+1)=\frac{n!}{(n-r)!}$$
組合せ
組合せ$$_nC_r=\frac{_nP_r}{r!}=\frac{n!}{r!(n-r)!}$$
和事象・余事象の確率
和事象・余事象の確立\(・P(A∪B)=P(A)+P(B)-P(A∩B)\)
\(・P(\overline{A})=1-P(A)\)
条件付き確率
条件付き確率$$P_A(B)=\frac{P(A∩B)}{P(A)}$$
整数の性質
ユークリッドの互除法
ユークリッドの互除法・2つの自然数の最大公約数を求める方法
・自然数aとbについてaをbで割ったときの余りをrとしたとき、aとbの最大公約数はbとrの最大公約数に等しい。これを繰り返し余りが0となったときの除数がaとbの最大公約数。
図形の性質
内角の二等分線と比
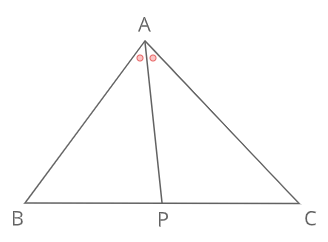
内角の二等分線と比 ∠Aの二等分線とBCの交点をPとすると
\(BP:PC=AB:AC\)
外角の二等分線と比
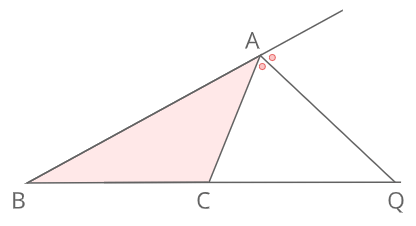
外角の二等分線と比点Aの外角の二等分線とBCの延長との交点をQとすると
\(BQ:QC=AB:AC\)
チェバの定理
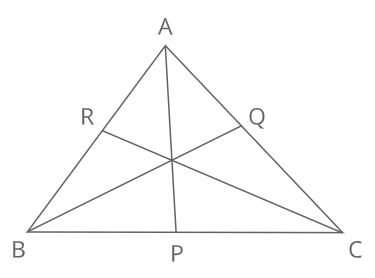
チェバの定理△ABCのBC、CA、AB上にそれぞれ点P、Q、Rがあるとき
\(\frac{PB}{CP}・\frac{RA}{BR}・\frac{QC}{AQ}=1\)
メネラウスの定理
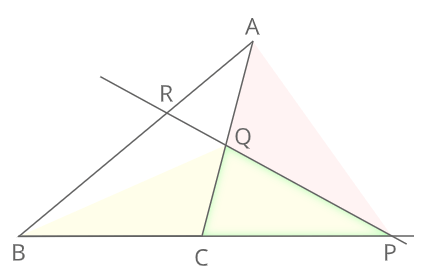
メネラウスの定理直線lとBC、CA、ABの交点をそれぞれP、Q、Rとすると
\(\frac{PB}{CP}・\frac{RA}{BR}・\frac{QC}{AQ}=1\)
円周角の定理
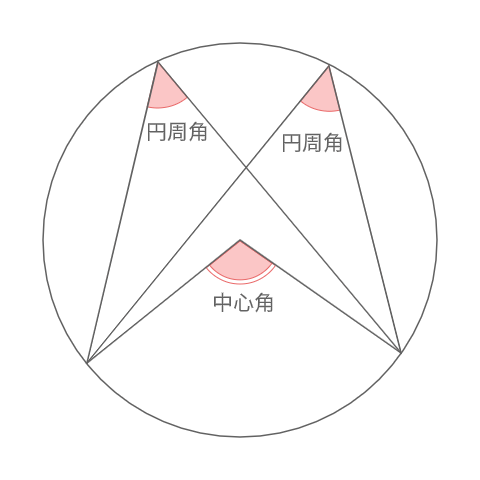
円周角の定理・同じ弧に対する円周角の大きさは中心角の大きさの半分
・同じ弧に対する円周角は等しい
円に内接する四角形
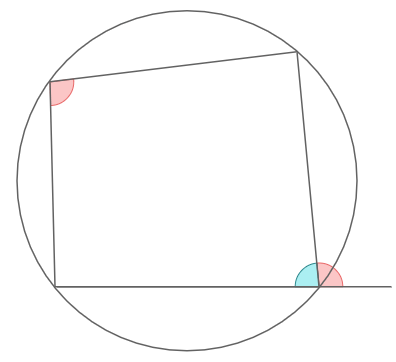
円に内接する四角形円に内接する四角形において
対角の和は180°
接弦定理
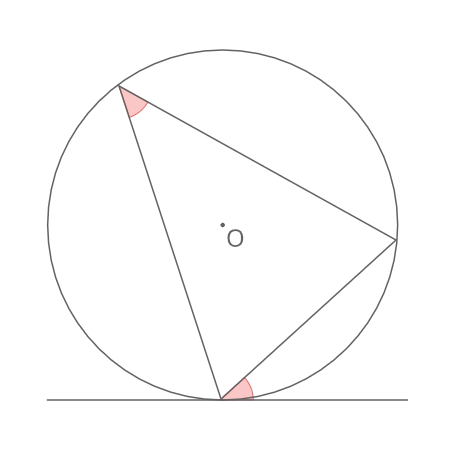
接弦定理円の接線とその接点を通る弦とがなす角は、その角内にある孤に対する円周角に等しい 。
方べきの定理1
方べきの定理1二直線の交点をPとし、直線と円の交点をA、BとC、Dとすると
\(PA・PB=PC・PD\)

方べきの定理2
方べきの定理2二直線の1直線と円の交点をA、Bとし、もう1直線と円がTで接するとき
\(PA・PB=PT^2\)



