分子や電荷が不均一に分布するとき,均一になろうとする力が働きます.これが拡散です.半導体では拡散による電流 (拡散電流)とドリフト電流があります.本記事では拡散電流について説明します.
拡散とは
温度や分子密度,電荷が不均一のとき,均一になろうとする力が働きます.これが拡散です.半導体でも図1のように電子密度が不均一に分布するとき,均一にしようとする力が電子に働きます.
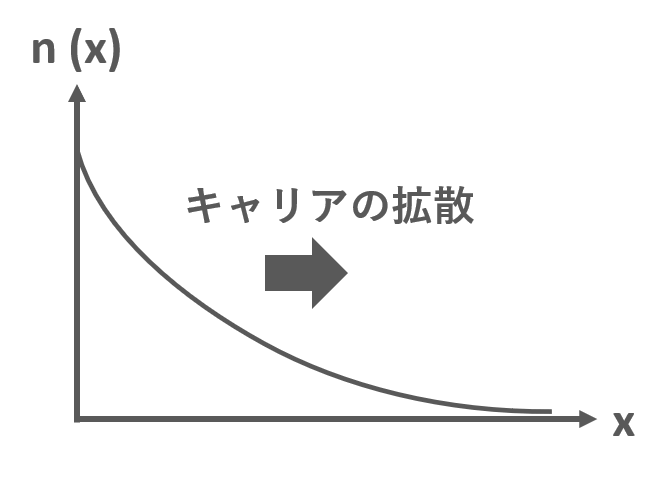
力が働いた電子は移動するため,電流が流れます.この拡散によって生じる電流を拡散電流といいます.
全体の拡散電流は電子と正孔による拡散を合わせた電流になるため,全体の拡散電流密度は以下のように示されます.
$$J=J_n+J_p=q\left\{D_n\frac{dn(x)}{dx}-D_p\frac{dp(x)}{dx}\right\}$$
\(J_n\):電子による拡散電流密度
\(J_p\):正孔による拡散電流密度
\(q\):電荷
\(n\):電子のキャリア密度
\(p\):正孔のキャリア密度
\(D_n\):電子の拡散係数
\(D_p\):正孔の拡散係数
上の式のように,電子と正孔が同じ向きに拡散すれば電流は互いに打ち消し合い,逆の向きに拡散すれば電流は足し合わせた値になります.また,拡散はキャリアの不均一で起きるため,不均一でなくなれば拡散電流も0になります.
拡散とドリフト
半導体では拡散電流だけではなく,電界よる電流 (ドリフト電流)も流れます.
場合によっては拡散電流とドリフト電流が互いに打ち消しあって平衡状態になります (電界をかけない場合のpn接合など).拡散電流とドリフト電流の平衡状態の式は電子の場合,拡散電流の式\(-qD\frac{dn(x)}{dx}\)とドリフト電流の式\(qn(x)\mu E\)から以下の式が成り立ちます.
$$-qn(x)\mu E=qD\frac{dn(x)}{dx}$$
\(n\): 電子のキャリア密度
\(\mu\): 移動度
\(E\): 電界
\(D\): 拡散係数
正孔でも同様の式が成り立ちます.
アインシュタインの関係
ここでは計算は省略しますが,電子の拡散とドリフトの関係の式,電子密度の近似式,位置エネルギーの微分とクーロン力の関係から以下のアインシュタインの関係が成り立ちます.
$$D_n=\mu _n\frac{kT}{q}$$
\(D_n\):電子の拡散係数
\(\mu_n\):電子の移動度
\(k\):ボルツマン定数
\(T\):絶対温度
\(q\):素電荷
アインシュタインの関係は移動度と拡散係数の関係を示し,正孔でも以下の式に示すように同様に成り立ちます.
$$D_p=\mu _p\frac{kT}{q}$$
\(D_p\):正孔の拡散係数
\(\mu_p\):正孔の移動度
拡散と再結合
ここからはより複雑になるため,拡散の基礎のみ知りたい方は以下を読まなくてもいいと思います.
キャリアの拡散を考える際,キャリアのの発生と再結合も考える必要があります.本章では,まずキャリアの発生・再結合について説明したあと,拡散と発生・再結合の関係について説明していきます.
キャリアの発生・再結合
キャリアは熱や光によって発生し,電子と正孔が再結合してキャリアは消える,を繰り返します.キャリアが励起されてから再結合するまでの時間を,キャリアの寿命時間 (ライフタイム)と呼びます.熱平衡状態と非熱平衡状態でのキャリアの発生・再結合について説明します.
熱平衡状態の場合
熱平衡状態ではキャリアの関係は以下のようになります.
$$n_0p_0=n_i^2$$
\(n_0\):熱平衡状態のときの電子密度
\(p_0\):熱平衡状態のときの正孔密度
\(n_i\):真性キャリア密度
伝導体にある電子はよりエネルギーの低い安定した準位に遷移しますが,価電子帯の正孔がある場合は伝導体の電子と価電子帯の正孔は再結合します
図2に熱平衡状態のp型半導体でのキャリアの発生と再結合の様子を示します.
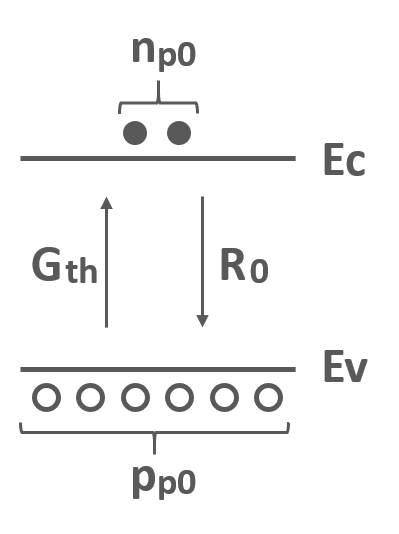
熱エネルギーによるキャリアの発生速度を\(G_{th}\),キャリアが再結合する速度を\(R_0\)とすると以下の式が成り立ちます.
$$G_{th}=R_0$$
\(G_{th}\):熱によるキャリアの発生速度
\(R_0\):キャリアの再結合速度
非熱平衡状態の場合
半導体に光が照射されたとき (非熱平衡状態)では,\(G_{th}=R_0\)が成り立たなくなります.図3に光が照射された場合 (非熱平衡状態)のキャリアの発生・再結合の様子を示します.
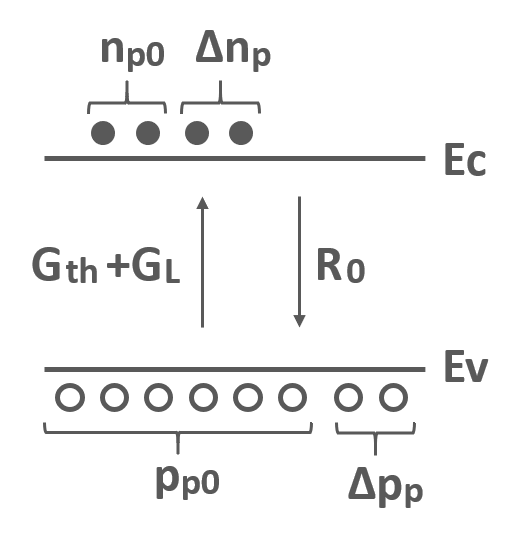
光によるキャリアの発生速度を\(G_L\)とするとキャリアの発生と再結合の関係は以下のように示されます.
$$G_{th}+G_L=R$$
\(G_{th}\):熱によるキャリアの発生速度
\(G_{L}\):光によるキャリアの発生速度
\(R\):キャリアの再結合速度
また光の照射によりp型半導体で発生した電子密度を\(\Delta n\),正孔密度を\(\Delta p\)とするとキャリアの関係は以下のようになります.
$$p_p=p_{p0}+\Delta p$$
$$n_p=n_{p0}+\Delta n$$
$$\Delta p=\Delta n$$
拡散と発生・再結合の関係
拡散と発生・再結合の関係について示します.
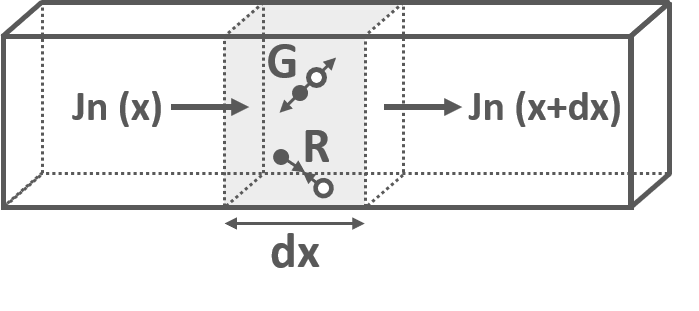
図4のようにp型半導体における単位長さあたりの少数キャリアの時間的変化は,以下の式で表されます.
$$\frac{\delta n_p(x,t)}{\delta t}=\frac{1}{q}\frac{J_n(x+dx)-J_n(x)}{dx}-R+G$$
\(n_p\):電子密度 (少数キャリアのキャリア密度)
\(J_n\):電子の電流密度
\(R\):再結合速度
\(G\):発生速度
\(q\):素電荷
詳しい計算は省きますが,拡散やドリフトの式を代入すると以下の連続の式が得られます.連続の式はキャリアの振る舞いを表す式です.n型半導体での少数キャリア (正孔)でも同様に考えられます.
$$\frac{\delta n_p(x,t)}{\delta t}=D_n\frac{\delta ^2n_p(x,t)}{\delta x^2}+\mu _nE\frac{\delta n_p(x,t)}{\delta x}-\frac{n_p(x,t)-n_0}{\tau _n}+G_L$$
片側から光を照射した場合の連続の式
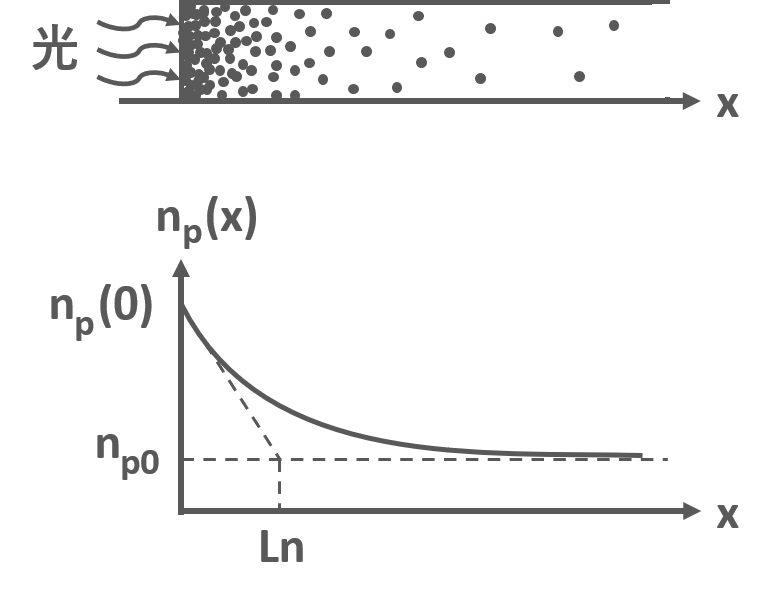
図5のようにp型半導体の片側から光を照射した場合について考えます.図のように片側から光を照射し続けた場合,表面で発生した少数キャリアは内部へ拡散しながら多数キャリアと再結合します.光が照射され続けた場合は定常状態となり,少数キャリア密度は時間的に変化しないため,先ほど示した連続の式から以下の式が導けます.
$$0=D_n\frac{d^2n_p(x)}{dx^2}-\frac{n_p(x)-n_0}{\tau _n}$$
また,境界条件n_p(0)=(定数),\(n_p(\infty)=n_{p0}\)より以下の解を得られます.
$$n_p(x)=n_{p0}+\{n_p(0)-n_{p0}\}exp(-\frac{x}{L_n})$$
\(n_p(x)\): 距離\(x\)での電子密度
\(n_{p0}\): 熱平衡状態での電子密度
\(n_p(0)\): 距離0での電子密度
\(L_n=\sqrt{D_n\tau _n}\): 拡散長 (拡散距離)
\(L_n=\sqrt{D_n\tau _n}\)は拡散長 (拡散距離)で光が照射された表面の少数キャリアのキャリア密度が\(1/e\ (\approx 36.8\ \%)\)になる長さのことを示します.n型半導体の少数キャリア (正孔)でも同様になります.
まとめ
- 拡散:不均一のときに均一になろうとする力によるキャリアの移動
- 拡散とドリフトの関係:\(-qn(x)\mu E=qD\frac{dn(x)}{dx}\)
- アインシュタインの関係:\(D=\mu \frac{kT}{q}\)
- 寿命時間 (ライフタイム):キャリアが励起されてから再結合するまでの時間
- 熱平衡状態での発生速度と再結合速度の関係:\(G_{th}=R_0\)
- 非熱平衡状態での発生速度と再結合速度の関係:\(G_{th}+G_L=R\)
- 連続の式:\(\frac{\delta n_p(x,t)}{\delta t}=D_n\frac{\delta ^2n_p(x,t)}{\delta x^2}+\mu _nE\frac{\delta n_p(x,t)}{\delta x}-\frac{n_p(x,t)-n_0}{\tau _n}+G_L\)
- 拡散長 (拡散距離):\(L_n=\sqrt{D_n\tau _n}\)



