半導体ではドリフトによって流れるドリフト電流と，拡散によって流れる拡散電流があります．本記事ではドリフト電流と，それに関係する散乱，平均緩和時間，移動度について解説します．
ドリフトとは
まずキャリアはマイナス電荷の電子，プラス電荷の正孔の二つがあります．半導体ではキャリアが移動することで電流が流れます．
半導体に電界をかけると，キャリアの運動に一定方向の偏りが生じます．これをドリフトと呼びます．電界Eによる力はF=QEで，Qはキャリアの電荷です．素電荷の大きさをq>0とすると，電子ではQ=−q，正孔ではQ=+qとなり，両者に働く力の向きは逆です．
キャリア散乱
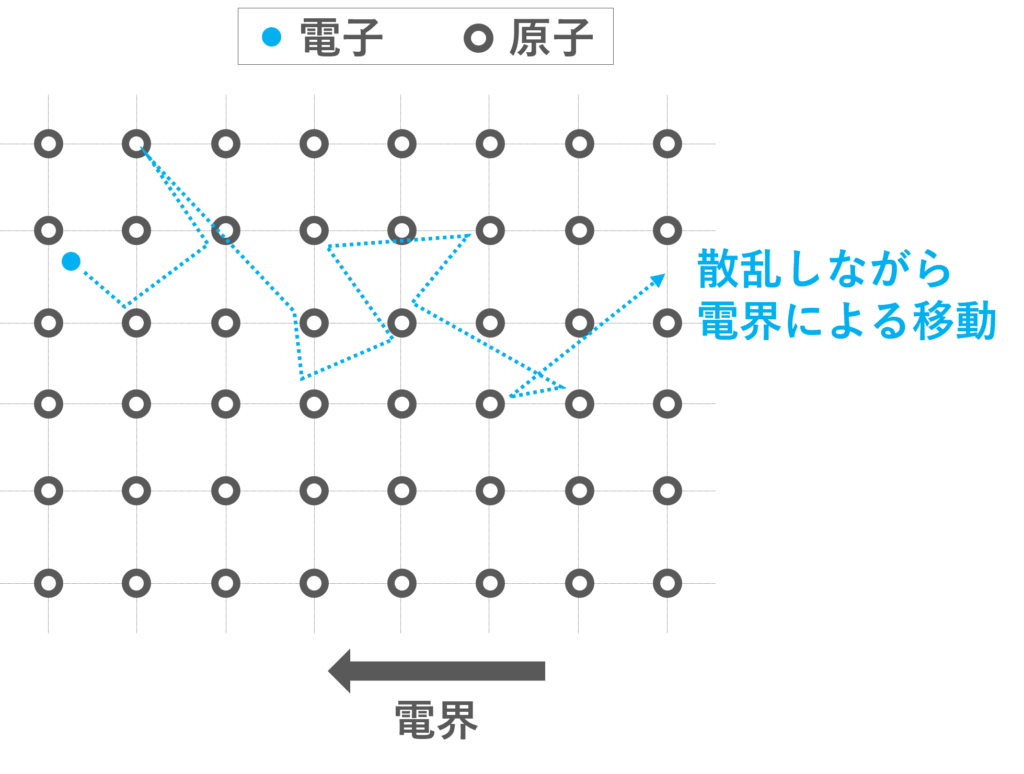
キャリアは電界によって移動 (ドリフト)するとき，散乱しながら移動します．散乱について説明します．
原子は熱エネルギーによって熱振動 (格子振動)してます．温度が高くなるにつれて格子振動も大きくなります．電子は格子振動している原子に不規則に衝突し，ランダムな方向に移動します．これが散乱で，キャリアは常に散乱してます．
電界や濃度勾配がないとき，キャリアは熱運動していても，集団全体の平均速度は0です．移動した道のりが0になるわけではありません．電界をかけると，散乱を繰り返しながらも平均速度に偏りが生じます．
平均緩和時間，移動度
平均緩和時間τは，散乱によってキャリアの運動量の偏りが失われる代表的な時間です．単純なモデルでは平均衝突時間に対応させ，力積と運動量の関係から以下のドリフト速度を求めます．
\(F\tau_n=m_n^*\overline{v_n} \\ ⇒ \overline{v_n}=\frac{F\tau_n}{m_n^*}=-\frac{q\tau_n}{m_n^*}E=-\mu_nE\)
\(\tau\)：平均緩和時間
\(\overline{v_n}\)：伝導電子の平均速度
\(m_n^*\)：伝導電子の有効質量
\(F\)：クーロン力
\(\mu_n\)：電子の移動度
比例係数\(\mu_n\)を移動度といいます．移動度は材料や製造方法だけでなく，温度や不純物濃度にも依存します．同じ弱い電界では，移動度が高いほどドリフト速度が大きくなります．強い電界では速度が飽和するため，電界に比例する関係から外れます．
正孔でも同様の関係が成り立ち，以下のようになります．
\(\overline{v_p}=\frac{F\tau_p}{m_p^*}=\frac{q\tau_p}{m_p^*}E=\mu_pE\)
\(\mu_p\)は正孔の移動度です．電子の方が正孔より移動速度が速く，\(\mu_n>\mu_p\)の関係があります．
２つのキャリア散乱
半導体でのキャリア散乱は，結晶を構成する原子の格子による格子散乱と，不純物による不純物散乱の二つがあります．
格子散乱は熱エネルギーによって振動している原子による散乱です．格子散乱は温度が高くなると散乱しやすくなり，移動度が小さくなります．定数\(k_1\)とすると，格子散乱のみの移動度\(\mu_L\)は以下のようになります．
\(\mu_L=k_1T^{-\frac{3}{2}}\)
不純物散乱は不純物が一般に正か負に帯電しており，キャリアを引き付けるか反発するためにキャリアが散乱します．不純物散乱は格子散乱とは反対に，温度が高くなるにつれてキャリアは速く移動するため，不純物による散乱は起こりにくくなります．不純物散乱のみを考慮した移動度\(\mu_I\)は，定数\(k_2\)，不純物密度\(N_I\)とすると以下のようになります．
\(\mu_I=k_2\frac{T^{\frac{3}{2}}}{N_I}\)
全体の散乱は以上の二つの散乱を足したものになるため，以下のようになります．
\(\frac{1}{\mu}=\frac{1}{\mu_L}+\frac{1}{\mu_I}\\⇒ \mu=\frac{1}{\frac{1}{\mu_L}+\frac{1}{\mu_I}}=\frac{1}{\frac{T^{\frac{3}{2}}}{k_1}+\frac{N_I}{k_2T^{\frac{3}{2}}}}\)
ドリフト電流
ドリフトにより流れる電流をドリフト電流といいます．キャリアは散乱しながら移動するため，伝導電子のドリフト電流密度\(J_n\)は移動度\(\mu_n\)より，以下のように求まります．
$$J_n=\frac{I}{S}=\frac{\Delta Q}{S\Delta t}=\frac{-qnSv_n\Delta t}{S\Delta t}=-qnv_n=qn\mu_nE$$
\(I\)：電流
\(S\)：断面積
\(Q\)：電荷
\(t\)：時間
\(q\)：素電荷
\(n\)：電子密度
\(v_n\)：移動する電子の平均速度
\(\mu_n\)：伝導電子の移動度
\(E\)：電界
正孔のドリフト電流密度も同様に求められます．ドリフト電流密度は伝導電子と正孔のドリフト電流密度の足し合わせて，以下のようになります．
$$J=J_n+J_p=q(n\mu_n+p\mu_p)E=\sigma E$$
\(\sigma\)：導電率
まとめ
- ドリフト：電界によるキャリアの移動
- キャリアの散乱：格子散乱と不純物散乱の二つがある
- 平均緩和時間：散乱によってキャリアの運動量の偏りが失われる代表的な時間
- 移動度：キャリアの電界をかけたときの移動のしやすさ
- ドリフト電流密度：\(J=J_n+J_p=q(n\mu_n+p\mu_p)E=\sigma E\)