MOSFETのドレイン電流\(I_{D}\)の式を導出していきます.MOSFETの基礎と動作を理解に役立ててください.(MOSFETの動作原理はこちら)
ドレイン電流 \(I_D\) (線形領域)
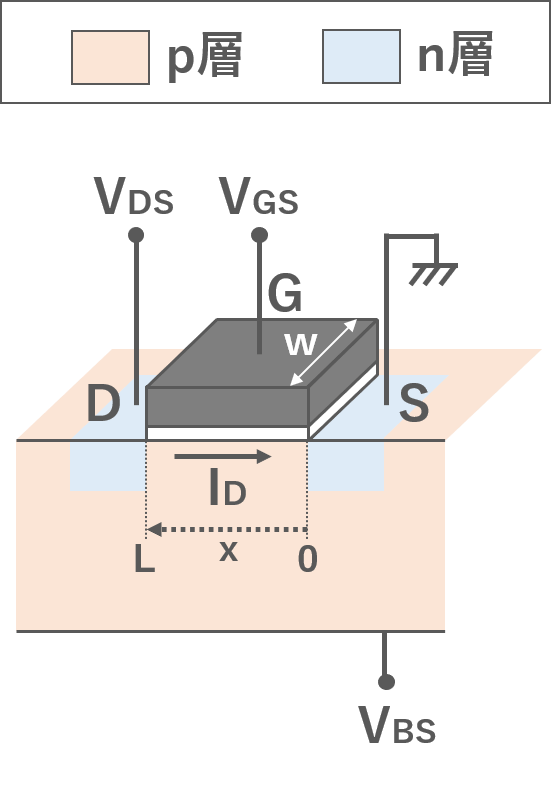
上図にnMOSの構造を示します.ゲートがオンのとき (ゲート電圧 \(V_{GS}\)がHのとき),ドレイン-ソース間で電流が流れるようになります.この状態で,ドレイン電圧\(V_{DS}\)を上げるほど,ドレイン電流も大きくなる領域を線形領域といいます.
先に答えを示しますが,線形領域でのドレイン電流は以下の通りです.次節で,nMOSの線形領域でのドレイン電流を導出をします (pMOSでも同様にして求められます).
線形領域でのドレイン電流 (nMOS)
$$I_{D}=\frac{W}{L}\mu_nC_{ox}\left[(V_{GS}-V_{TH})V_{DS}-\frac{1}{2}V_{DS}^2\right]$$
線形領域でのドレイン電流 (pMOS)
$$I_{D}=-\frac{W}{L}\mu_pC_{ox}\left[(V_{GS}-V_{TH})V_{DS}-\frac{1}{2}V_{DS}^2\right]$$
- \(W\):ゲート幅
- \(L\):ゲート長
- \(\mu_n\):電子の移動度
- \(\mu_p\):ホールの移動度
- \(C_{ox}\):ゲート容量
- \(V_{GS}\):ゲート電圧
- \(V_{TH}\):しきい値電圧
- \(V_{DS}\):ドレイン電圧
式の導出 (線形領域・nMOS)
nMOSの線形領域での,ドレイン電流\(I_D\)の導出をしていきます.改めてnMOSの構造図を下に示します.

ゲート下にはゲート電圧 \(V_{GS}\)から,しきい値電圧 \(V_{TH}\)を引いた電圧がかかっています.また,ドレインに電圧\(V_{DS}\)をかけると,上図の位置\(x\)によってゲート下に電圧\(V(x)\)がかかります.\(Q=CV\)の関係より,これら電圧とゲート容量\(WC_{ox}\) (\(Wはゲート幅\))を用いると,\(x\)のゲート下で誘起された電荷は
\(Q(x)=-WC_{ox}(V_{GS}-V(x)-V_{TH}) ①\)
となります.電子の移動度\(\mu_n\)より,\(x\)での電子の速度は\(u(x)=-\mu_nE(x)\)となります (移動度についてはこちら).また電流\(I\)は,電荷量\(Q\)と電荷の平均速度の積から求めることができます.これらを用いるとドレイン電流\(I_D\)は
\(I_D=Q(x)u(x)=Q(x)(-\mu_nE(x))=Q(x)\mu_n\frac{dV(x)}{dx} ②\)
① ②より
\(I_D=WC_{ox}(V_{GS}-V(x)-V_{TH})\mu_n\frac{dV(x)}{dx}\)
また\(V(0)=0\),\(V(L)=V_{DS}\)より
\(\displaystyle \int_{0}^{L}I_Ddx=W\mu_nC_{ox}\displaystyle \int_{0}^{V_{DS}}(V_{GS}-V_{TH}-V(x))dV(x) \)
⇒\([I_D]_0^L=W\mu_nC_{ox}[(V_{GS}-V_{TH})V(x)-\frac{1}{2}V(x)^2]_0^{V_{DS}}\)
⇒\(LI_D=W\mu_nC_{ox}[(V_{GS}-V_{TH})V_{DS}-\frac{1}{2}V_{DS}^2]\)
⇒\(I_D=\frac{W}{L}\mu_nC_{ox}[(V_{GS}-V_{TH})V_{DS}-\frac{1}{2}V_{DS}^2]\)
以上のように,nMOSの線形領域での,ドレイン電流\(I_D\)の導出をしました.
ドレイン電流 \(I_D\) (飽和領域)
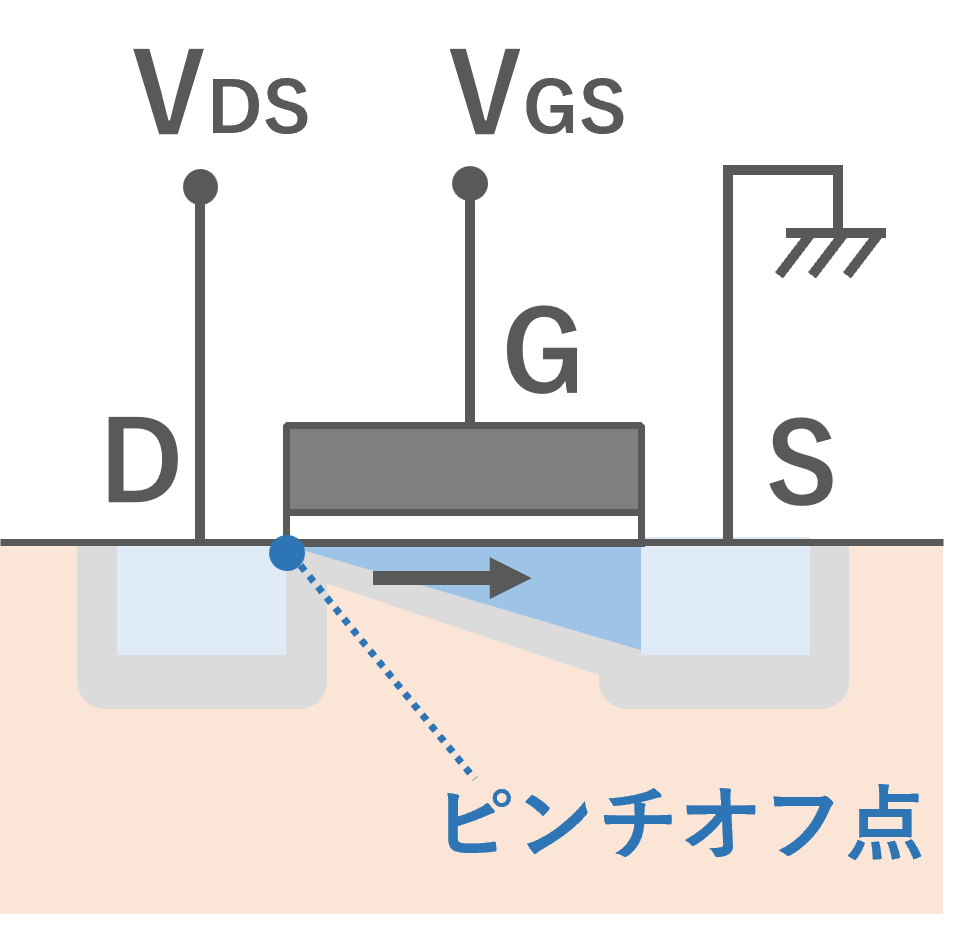
上図にnMOSの構造を示します.ゲートがオンのとき (ゲート電圧 \(V_{GS}\)がHのとき),ドレイン-ソース間で電流が流れるようになります.この状態で,ドレイン電圧\(V_{DS}\)を線形領域からさらに上げると,あるときからドレイン電流が増えなくなります (チャネル長変調効果なしの場合).このドレイン電流が飽和した領域を,飽和領域といいます.これはドレイン電圧\(V_{DS}\)によって,ドレイン近くで反転層がなくなるピンチオフ点が現れるためです.
先に答えを示しますが,飽和領域でのドレイン電流は以下の通りです.次節で,nMOSの飽和領域でのドレイン電流を導出をします (pMOSでも同様にして求められます).
飽和領域でのドレイン電流 (nMOS,チャネル長変調効果なし)
$$I_{D}=\frac{1}{2}\frac{W}{L}\mu_nC_{ox}(V_{GS}-V_{TH})^2$$
飽和領域でのドレイン電流 (pMOS,チャネル長変調効果なし)
$$I_{D}=- \frac{1}{2}\frac{W}{L}\mu_pC_{ox}(V_{GS}-V_{TH})^2$$
式の導出 (飽和領域)
nMOSの飽和領域でのドレイン電流 (チャネル長変調効果なしの場合)の導出をしていきます (チャネル長変調効果ありの場合の式はMOSFETの基礎④【チャネル長変調効果】で導出).
\(V_{DS}\)が大きくなると上図のピンチオフ点では誘起電荷がなくなるため,ピンチオフ点\(x_p\)では
\(Q(x_p)=-WC_{ox}(V_{GS}-V(x_p)-V_{TH})=0\)
となるため,以下が成り立つ
\(V(x_p)=V_{GS}-V_{TH}\)
よって線形領域のドレイン電流の式で\(V_{DS}=V_{GS}-V_{TH}\)とすればいいため
\(I_D=\frac{1}{2}\frac{W}{L}\mu_nC_{ox}(V_{GS}-V_{TH})^2\)
となります.
ドレイン電流のグラフ

上で求めた式をグラフにすると上図のようになります.
まとめ
線形領域でのドレイン電流 (nMOS)
$$I_{D}=\frac{W}{L}\mu_nC_{ox}\left[(V_{GS}-V_{TH})V_{DS}-\frac{1}{2}V_{DS}^2\right]$$
線形領域でのドレイン電流 (pMOS)
$$I_{D}=-\frac{W}{L}\mu_pC_{ox}\left[(V_{GS}-V_{TH})V_{DS}-\frac{1}{2}V_{DS}^2\right]$$
飽和領域でのドレイン電流 (nMOS,チャネル長変調効果なし)
$$I_{D}=\frac{1}{2}\frac{W}{L}\mu_nC_{ox}(V_{GS}-V_{TH})^2$$
飽和領域でのドレイン電流 (pMOS,チャネル長変調効果なし)
$$I_{D}=- \frac{1}{2}\frac{W}{L}\mu_pC_{ox}(V_{GS}-V_{TH})^2$$



