電気回路の用語集③です.復習として,電子回路に必要な基礎知識を示しています.知らなかったり忘れている内容がある場合は,電子回路を勉強する前に復習することをおすすめします.
- 電気回路の用語集①(電力,有効数字,単位など)
- 電気回路の用語集②(抵抗,インピーダンスなど)
- 電気回路の用語集③今ココ!
- 電子回路の基礎まとめ!
キルヒホッフの法則
キルヒホッフの法則は、電気回路における基本的な法則で、電流と電圧の関係を理解するための基盤となります。主に2つの法則があります。
- キルヒホッフの電流法則(キルヒホッフの第1法則)
この法則は、「回路内の任意の点で流れ込む電流の合計は、流れ出る電流の合計に等しい」というものです。つまり、電流は保存されるため、回路の各接続点(ノード)で電流が増減することはないという原理です。これにより、回路の電流の分布を計算することができます。 - キルヒホッフの電圧法則(キルヒホッフの第2法則)
この法則は、「回路内の任意の閉じたループ(回路経路)において、電圧の上昇と下降の総和はゼロになる」というものです。つまり、回路を一周してもエネルギーの総和は保存され、電源から供給されるエネルギーは、抵抗などの要素で消費されるエネルギーに等しいという原理です。
これらの法則は、回路解析において非常に重要で、複雑な回路の電流や電圧を計算する際に広く使用されます。
重ね合わせの理
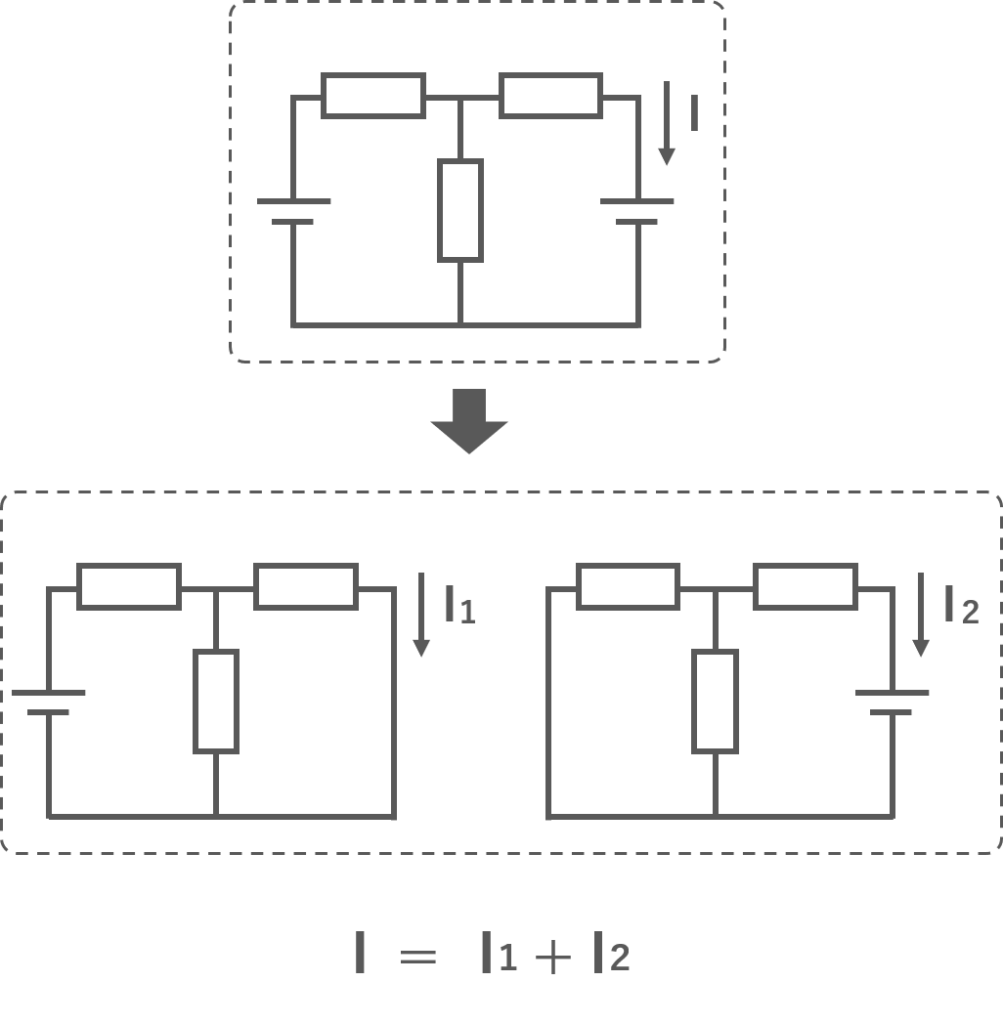
重ね合わせの理を上図に示します.重ね合わせは複数の電源を持つ回路の,ある点で流れる電流は,各電源ごとに求めたその点で流れる電流の総和に等しいという理論です.重ね合わせの理は受動素子のみで構成される回路で成り立ちます (能動素子でも受動素子のみで構成される等価回路に変換する場合は成り立つ).
テブナンの定理
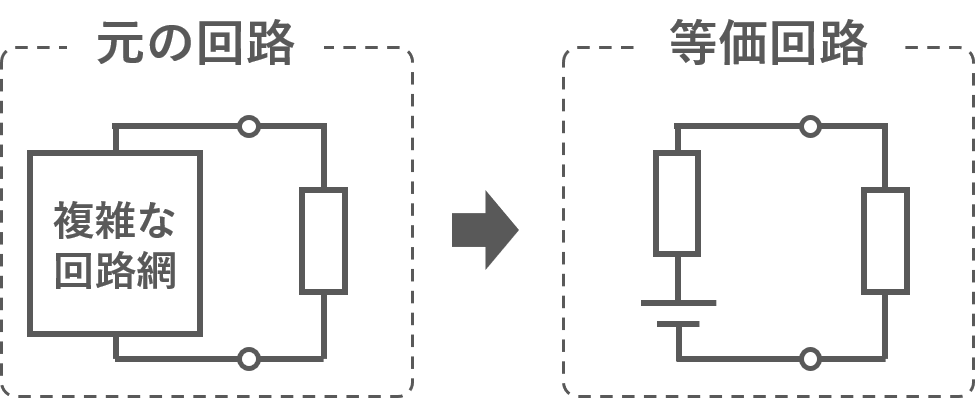
テブナンの定理は上図のように複雑な回路を簡単な電源とインピーダンスの等価回路に変換してあるインピーダンスに流れる電流を求める定理です.複雑な線形回路を単純な回路に置き換えて解析を簡単にするための定理です。この定理によれば、任意の線形回路は、特定の2端子回路(負荷が接続される端子)に対して、次の2つの要素だけで置き換えることができます。
- テブナンの電圧(V_th)
これは、負荷端子における開放電圧、すなわち回路を切り離した状態で測定される電圧です。テブナンの定理における「電圧源」に相当します。 - テブナンの抵抗(R_th)
これは、負荷端子を開放した状態で、回路内のすべての電源を無効化(電圧源は短絡、電流源は開放)したときの抵抗値です。回路内の抵抗がどれくらいの影響を与えるかを示します。
テブナンの定理を利用すると、複雑な回路を簡略化でき、負荷にかかる電圧や電流をより簡単に計算することが可能になります。特に、回路解析や設計において、効率的に計算を行うために活用される重要な手法です。
ノートンの定理
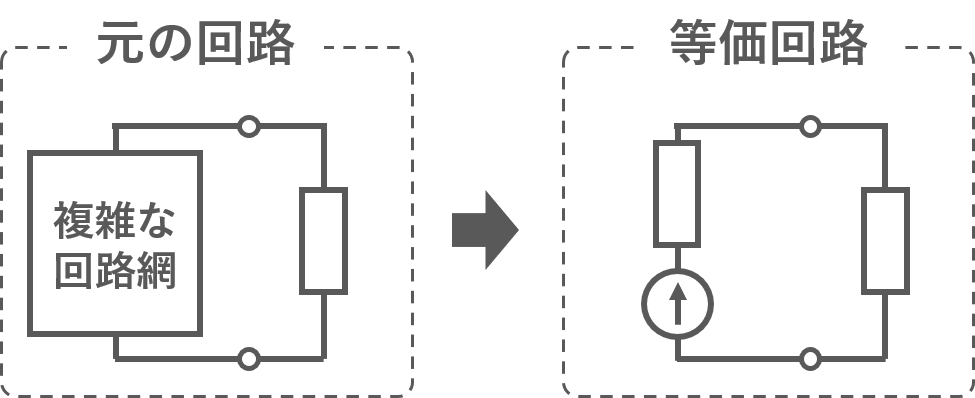
ノートンの定理はテブナンの定理に似た定理で,図のように複雑な回路を簡単な電流源とアドミタンスの等価回路に変換してあるアドミタンスにかかる電圧を求める定理です.
集中定数回路と分布定数回路
集中定数回路と分布定数回路は、回路の特性に基づく2つの異なるモデルです。これらは、回路内での抵抗、インダクタンス、キャパシタンスの分布に関する仮定に基づいています。
集中定数回路は、回路内のすべての抵抗、インダクタンス、キャパシタンスを一箇所に集めてモデル化するアプローチです。このモデルでは、回路内の各素子が理想的に一つの位置に配置され、回路全体での振る舞いを簡単に解析できます。通常、低周波数(または小さな距離での信号伝送)で使われ、各素子の影響を個別に計算することが可能です。このモデルは、回路内での素子間の時間的遅れや信号の伝播を無視するため、シンプルで計算が容易です。
分布定数回路は、回路内の抵抗、インダクタンス、キャパシタンスが均等に分布していると仮定しているモデルです。このモデルは、特に高周波や長い伝送ライン(例えば、高速通信回路)において重要です。信号の伝播において、各素子の影響が位置によって異なるため、信号の遅延や反射などが考慮されます。分布定数回路は、回路全体を線形な媒質として扱い、信号が伝わる時間遅延を考慮して解析するため、より現実的な高周波回路の設計に適しています。
両者の違いは、回路素子の配置の仕方と、それに伴う解析方法にあります。低周波回路では集中定数回路が簡便で有効ですが、高周波や長距離の伝送には分布定数回路が重要となります。
まとめ
- キルヒホッフの第1法則:流れ込む電流の総和は出ていく電流の総和に等しい
- キルヒホッフの第2法則:回路で一回りしたときに起電力の総和と電圧降下の総和は等しい
- 重ね合わせの理:複数の電源を持つ回路のある点で流れる電流は,各電源ごとに求めたその点で流れる電流の総和に等しい
- テブナンの定理:複雑な回路を簡単な電源とインピーダンスの等価回路に変換してあるインピーダンスに流れる電流を求める定理
- ノートンの定理:複雑な回路を簡単な電流源とアドミタンスの等価回路に変換してあるアドミタンスにかかる電圧を求める定理
- 集中定数回路:導線の影響を考慮しない回路
- 分布定数回路:導線の影響を考慮した回路



