高校物理の力学の定義・法則などをまとめました。勉強に役立ててもらえれば幸いです。
運動量
運動量・力積
運動量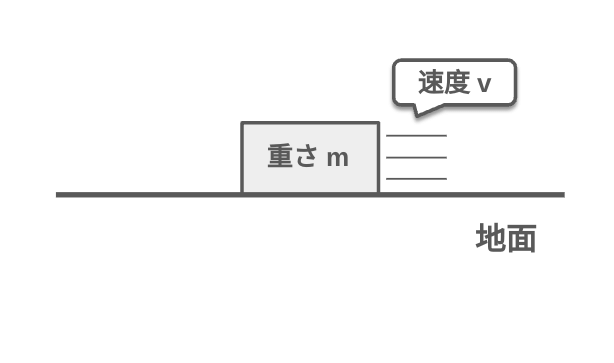とは、物体の質量と速度の積で表される物理量です。運動量（p）は、質量（m）と速度（v）の積で計算され、p = m × v となります。運動量は、物体の運動の勢いを示す指標です。例えば、質量2kgの物体が3m/sの速度で動いている場合、その運動量は6kg・m/sとなります。力積とは、力が物体に作用した時間の積で、運動量の変化を示します。力積（I）は、力（F）と時間（t）の積で表され、I = F × t です。
運動量保存の法則
運動量保存の法則は、外部から力が加わらない限り、運動量の総量が一定であることを示します。例えば、衝突する2つの物体がある場合、衝突前の運動量の合計は衝突後の運動量の合計と等しくなります。具体的には、質量3kgの物体が4m/sで右に動き、質量2kgの物体が3m/sで左に動いて衝突する場合、衝突前の運動量は3kg×4m/s + 2kg×(-3m/s) = 6kg・m/sです。衝突後も、この運動量の合計は変わりません。
物体の分裂
物体の分裂とは、一つの物体が複数の物体に分かれる現象です。運動量保存の法則により、分裂前後の運動量の総和は等しくなります。例えば、質量5kgの物体が静止している状態で、2kgと3kgの物体に分裂するとします。このとき、2kgの物体が左に2m/sで動いた場合、3kgの物体は右に何m/sで動くでしょうか？分裂前の運動量は0なので、2kg×(-2m/s) + 3kg×v = 0 となり、v = 4/3 m/s です。
反発係数
反発係数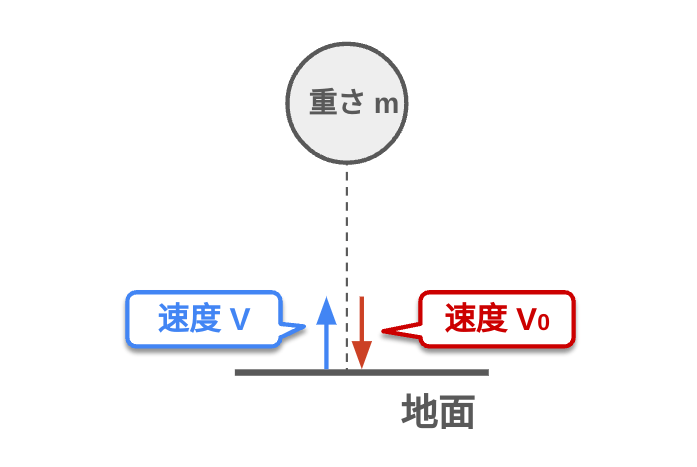
反発係数（e）とは、衝突後の物体の速度の比率を示す指標です。具体的には、e = |v2′ – v1’| / |v1 – v2| で表されます。ここで、v1とv2は衝突前の速度、v1’とv2’は衝突後の速度です。反発係数が1に近いと弾性衝突（完全に弾む）、0に近いと非弾性衝突（弾まない）を示します。例えば、反発係数が0.8の物体同士が衝突すると、衝突後の速度変化は元の速度の80%となります。
2物体の反発係数
2物体の反発係数は、衝突後の相対速度と衝突前の相対速度の比率で求められます。例えば、質量2kgの物体Aが5m/sで右に動き、質量3kgの物体Bが3m/sで左に動いて衝突するとします。衝突後、Aの速度が2m/s、Bの速度が1m/sになった場合、反発係数eは |1m/s – 2m/s| / |5m/s – (-3m/s)| = 0.125 です。これにより、衝突の弾性の程度を評価できます。
運動量保存と力学的エネルギー
運動量保存の法則と力学的エネルギーの保存は、物体の運動の分析に重要です。運動量は常に保存されますが、力学的エネルギーは弾性衝突と非弾性衝突で異なります。弾性衝突では、運動エネルギーも保存されます。例えば、2つの弾性ボールが衝突する場合、衝突前後で運動エネルギーと運動量の総和が同じです。一方、非弾性衝突では、エネルギーの一部が熱や変形に変わり、運動エネルギーは減少しますが、運動量は依然として保存されます。
円運動
円運動
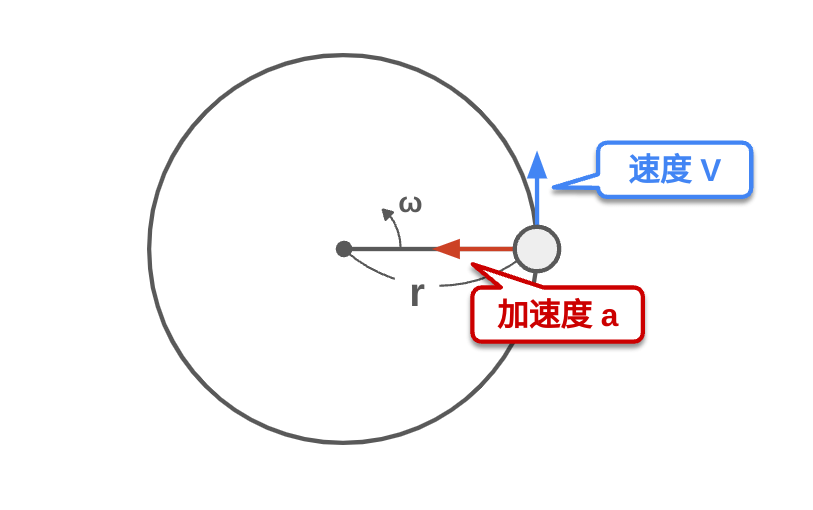
円運動とは、物体が円形の軌道を描いて動く運動です。この運動では、物体は常に中心に向かう力（向心力）を受けています。例えば、糸に結んだ石を振り回すと、石は円運動をします。このとき、糸が引っ張る力が向心力となります。速度が一定でも、方向が常に変わるため、加速度が存在します。この加速度を向心加速度と呼びます。
遠心力
遠心力は、円運動をする物体が外側に押し出されるように感じる力です。実際には、これは物体が慣性により直進しようとする力に対する反作用です。例えば、車がカーブを曲がるとき、体が外側に押し出されるように感じますが、これは遠心力の作用です。遠心力は、円運動の速さや曲率半径に依存します。
単振動
単振動
単振動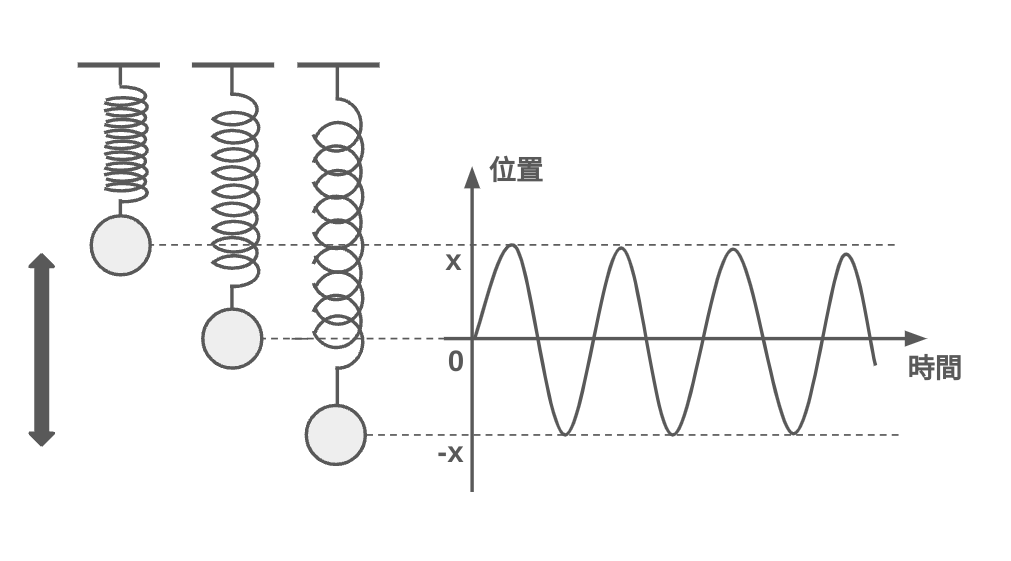とは、物体が一定の周期で往復する運動のことです。例えば、ばねに吊るされた重りや、振り子の運動が単振動に該当します。これらの運動では、物体は常に平衡位置に戻ろうとする力を受けます。この力を復元力と呼びます。単振動の周期や振幅は、ばね定数や重力加速度に依存します。
ばね振り子
ばね振り子とは、ばねに取り付けられた質量が上下に振動する運動です。例えば、垂直に吊るしたばねの先に重りを取り付けて上下に引っ張ると、ばね振り子の運動が観察できます。この運動では、ばねの伸び縮みによる復元力が重りを平衡位置に戻そうとします。ばね定数と質量により、振動の周期が決まります。
単振り子
単振り子は、糸の先に重りを取り付けた振り子のことです。例えば、時計の振り子が単振り子の一例です。単振り子の運動は、重りが振り子の中心から一定の角度を描いて往復する運動です。この運動の周期は、糸の長さと重力加速度に依存しますが、振幅が小さい場合に限ります。周期は振幅に依存しない特徴があります。
単振動のエネルギー
単振動では、運動エネルギーと位置エネルギーが交互に変換されます。例えば、ばね振り子の場合、重りが最も上に来るときには運動エネルギーが最小で、位置エネルギーが最大です。一方、重りが平衡位置を通過するときには、運動エネルギーが最大で、位置エネルギーが最小になります。これにより、全エネルギーは一定に保たれます。
万有引力
ケプラーの法則
ケプラーの法則は、惑星の運動を説明する3つの法則です。第一法則は「楕円軌道の法則」で、惑星は太陽を焦点とする楕円軌道を描きます。第二法則は「面積速度一定の法則」で、惑星と太陽を結ぶ線が一定の面積速度で掃かれます。つまり、惑星は太陽に近づくと速く、遠ざかると遅く動きます。第三法則は「調和の法則」で、惑星の公転周期の二乗は軌道の長半径の三乗に比例します。これにより、惑星の運動を正確に予測できます。
万有引力
万有引力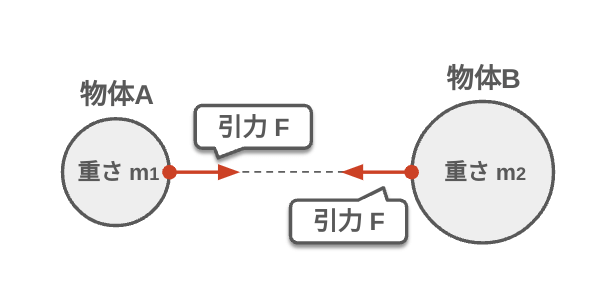は、すべての質量を持つ物体が互いに引き合う力です。ニュートンの万有引力の法則によると、引力の大きさは2つの物体の質量の積に比例し、距離の二乗に反比例します。例えば、地球と月はお互いに引き合っており、これが月が地球の周りを回る原因です。この力は、宇宙のすべての天体の運動にも関わっています。
万有引力による位置エネルギー
万有引力による位置エネルギーは、高い位置にある物体が持つエネルギーです。地球上で物体を持ち上げると、その物体は位置エネルギーを持ちます。このエネルギーは、物体が持ち上げられた高さと地球の質量に依存します。例えば、高いビルからボールを落とすと、位置エネルギーが運動エネルギーに変わり、ボールは加速して地面に向かいます。
慣性力
慣性力
慣性力は、物体が直線運動を続けようとする力です。ニュートンの第一法則によると、外部から力が加わらない限り、物体はその運動状態を保ちます。例えば、急に止まる電車の中で前に投げ出されるのは、慣性力のためです。これは、乗客が直線運動を続けようとする結果です。
遠心力
遠心力は、円運動する物体が外側に押し出されるように感じる力です。実際には、これは物体が直線運動を続けようとする慣性力に対する反作用です。例えば、回転するメリーゴーランドの上で外側に押し出される感じが遠心力の例です。この力は、回転速度や半径に依存します。
コリオリ力
コリオリ力は、回転する座標系で観測される見かけの力です。例えば、地球の自転により、北半球では風が右に、南半球では左に曲がります。この力は、物体の速度と回転の角速度に依存します。コリオリ力は、気象現象や海流の動きにも大きな影響を与えています。
まとめ
本記事では高校物理の「力学」の定義や法則の③をまとめました。
力学は、物体の動きや力の働きを研究する物理学の分野です。物体の運動やその原因となる力を理解することで、自然界の様々な現象を説明できます。例えば、リンゴが木から落ちる現象や車が走るときの加速など、日常生活で見られる多くの動きは力学で説明できます。ニュートンの運動の法則が力学の基本であり、これにより物体の運動状態がどう変わるかを予測できます。力学は、工学や建築、スポーツなど、多くの分野で応用されており、私たちの生活に密接に関わっています。
本記事で少しでも高校物理の「力学」の学習に役立てていたら幸いです。
その他の高校物理まとめは下記の黄色い枠のリンクから↓
