高校物理の力学の定義・法則などをまとめました。勉強に役立ててもらえれば幸いです。
力
力学とは

力学は、物体の動きや力の働きを研究する物理学の分野です。物体の運動やその原因となる力を理解することで、自然界の様々な現象を説明できます。例えば、リンゴが木から落ちる現象や車が走るときの加速など、日常生活で見られる多くの動きは力学で説明できます。ニュートンの運動の法則が力学の基本であり、これにより物体の運動状態がどう変わるかを予測できます。力学は、工学や建築、スポーツなど、多くの分野で応用されており、私たちの生活に密接に関わっています。
力
力は物体の運動状態を変える原因となるもので、大きさと方向を持つベクトル量です。力が加わると、物体は加速したり、方向を変えたりします。例えば、サッカーボールを蹴るとき、足がボールに力を加えてボールが飛びます。力の単位はニュートン(N)で、質量1kgの物体に1m/s²の加速度を与える力として定義されます。力には重力、摩擦力、張力などがあり、それぞれ異なる状況で物体に影響を与えます。
力の合成・分解
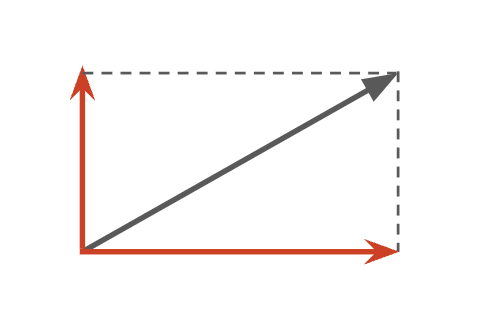
力の合成とは、複数の力を一つの力にまとめることです。例えば、二人が異なる方向から物体を押す場合、その合成力を求めることで物体の動きを予測できます。力の分解とは、一つの力を二つ以上の成分に分けることです。例えば、斜面を滑り降りる物体には、重力を斜面方向と垂直方向に分解して考えます。これにより、力の影響を正確に分析できます。力の合成と分解は、物理現象を理解するための基本的な技術です。
力のつり合い
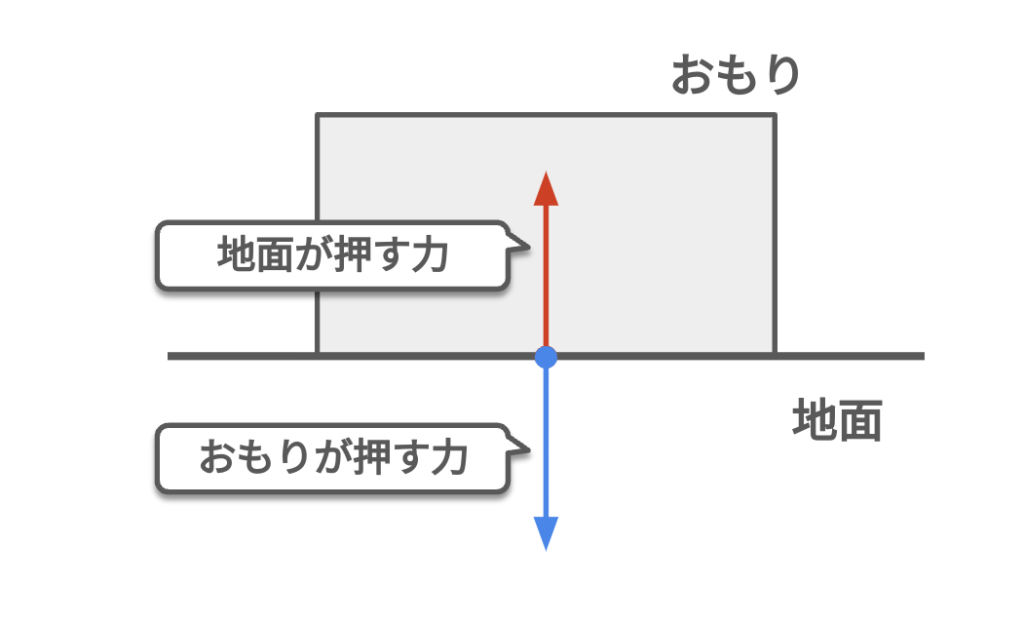
力のつり合いとは、物体に働く全ての力が互いに打ち消し合い、物体が静止する状態です。例えば、テーブルの上に置かれた本は、重力とテーブルからの反作用が釣り合っているため動きません。ニュートンの第一法則によれば、力がつり合っていると物体は静止し続けるか、等速直線運動を続けます。力のつり合いの原理は、建築物の安定性や機械の設計など、さまざまな場面で応用されています。
作用・反作用の法則

作用・反作用の法則は、ニュートンの第三法則として知られています。これは、物体が他の物体に力を加えるとき、同じ大きさで逆方向の力が返ってくることを示します。例えば、ボールを壁に投げると、壁から反作用の力を受けてボールは跳ね返ります。この法則は、ロケットの推進原理にも応用されています。ロケットは燃料を噴射し、その反作用で前進します。このように、作用・反作用の法則は、さまざまな運動の基本原理を理解するために重要です。
張力
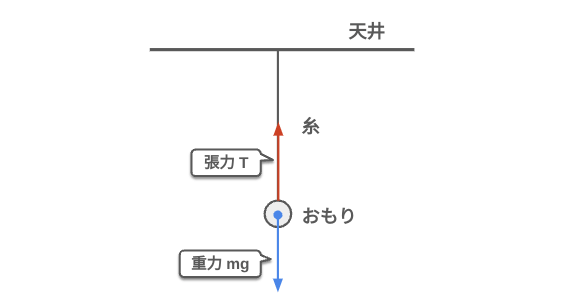
張力は、物体を引っ張る力で、糸やロープなどが引っ張られているときに発生します。例えば、ブランコに乗ると、ロープに張力が生じて体を支えます。張力は、物体の質量や加速度によって変わり、常に引っ張られる方向に働きます。張力の計算では、物体に働く他の力とバランスを取ることが重要です。張力は、建築や橋梁の設計など、さまざまな構造物の安定性を確保するために重要な概念です。
上手の場合、下記の式が成り立ちます。
$$T=mg$$
弾性力・摩擦力
弾性力・フックの法則
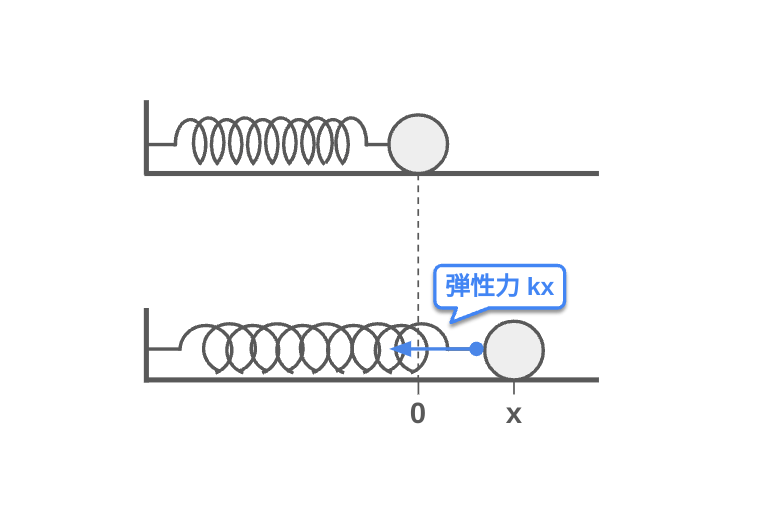
弾性力は、変形した物体が元の形に戻ろうとする力です。例えば、バネを引っ張ると元に戻ろうとする力が働きます。フックの法則は、弾性力が変形の大きさに比例することを示しています。これは、バネの伸び縮みが元の長さに対してどれだけ変わったかによって決まります。フックの法則は、F = kxの式で表され、ここでFは弾性力、kはバネ定数、xは変形の大きさです。弾性力とフックの法則は、機械や建築の設計で重要です。
摩擦力
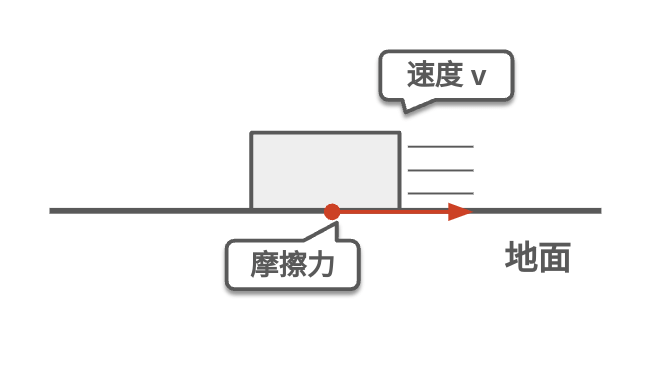
摩擦力は、物体が接触面を滑るときに生じる抵抗力です。例えば、机の上に置かれた本を押すとき、摩擦力が本の動きを妨げます。摩擦力には、静止摩擦力と動摩擦力の二種類があります。静止摩擦力は、物体が静止しているときに働き、動き始めるのを防ぎます。動摩擦力は、物体が動いているときに働き、滑るのを遅くします。摩擦力は、物体の質量や接触面の性質によって変わり、日常生活や工業分野で重要な役割を果たします。
静止摩擦力・動摩擦力
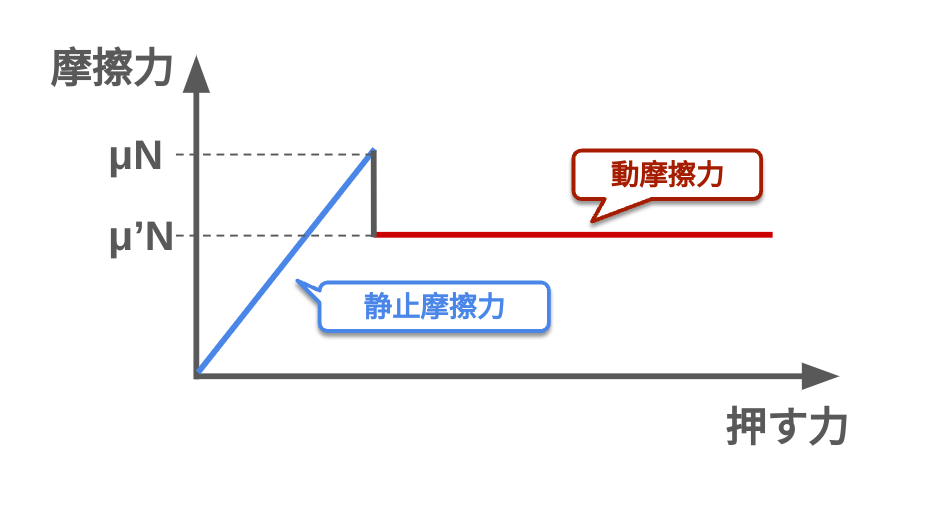
静止摩擦力は、物体が静止しているときに働く摩擦力です。例えば、斜面に置いた箱が滑り落ちないのは、静止摩擦力が重力に対抗しているためです。動摩擦力は、物体が動き始めたときに働く摩擦力で、静止摩擦力よりも一般的に小さくなります。例えば、机の上の本を押して動かすと、最初は大きな力が必要ですが、動き始めると少ない力で動かせます。静止摩擦力と動摩擦力の理解は、物体の動きや安定性を考える上で重要です。
摩擦角
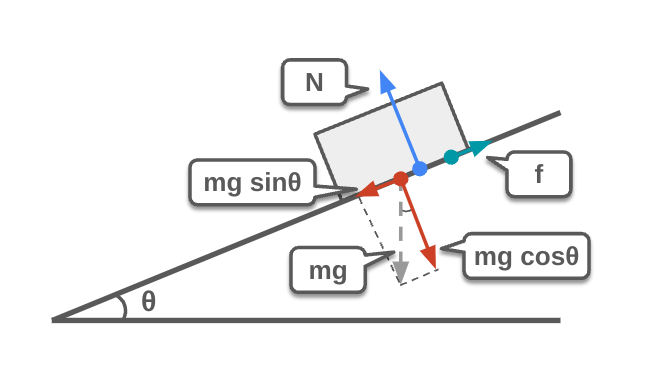
摩擦角は、物体が滑り始める角度を示す角度です。例えば、箱を斜面に置いて徐々に傾けていくと、ある角度で滑り始めます。この角度が摩擦角です。摩擦角は、静止摩擦係数と密接に関連しており、斜面の傾きが摩擦力と重力のバランスを崩したときに物体が滑り始めます。摩擦角の概念は、道路の設計や運動の安定性を考える際に役立ちます。これにより、物体が滑りやすいかどうかを予測できます。
パスカルの原理・浮力
パスカルの原理
パスカルの原理は、液体や気体の圧力が均等に伝わることを示しています。例えば、密閉された容器に水を入れ、その一部に圧力を加えると、その圧力が全体に均等に伝わります。この原理は、油圧機器やブレーキシステムで利用されています。パスカルの原理を使うと、小さな力で大きな力を生み出すことができ、効率的な力の伝達が可能です。これにより、重い物体を持ち上げたり、車を安全に停止させたりすることができます。
水圧
水圧は、水中で働く圧力で、深さに比例して増加します。例えば、ダムの底部では水圧が高くなり、ダムの壁には大きな力がかかります。水圧は、深さだけでなく、水の密度にも依存します。パスカルの原理により、水圧はあらゆる方向に均等に伝わります。この原理を理解することで、潜水艦の設計やダムの建設、パイプラインの設計など、水圧に関する問題を解決することができます。
浮力
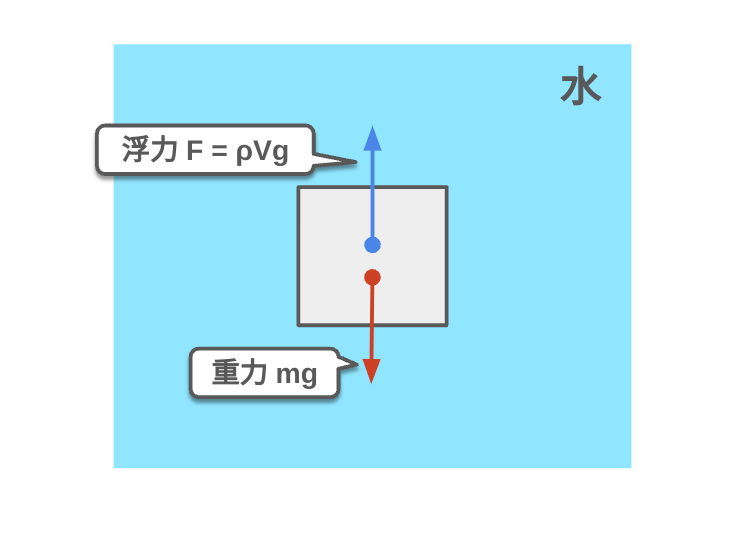
浮力は、液体や気体の中にある物体が受ける上向きの力です。アルキメデスの原理により、浮力は物体が押しのけた流体の重さに等しいとされています。例えば、ボートが水に浮かぶのは、ボートが押しのけた水の重さがボートの重さと釣り合うからです。風船が空中に浮かぶのも同じ原理で、風船の中の軽いガスが空気を押しのけ、その重さ分だけ上向きの浮力が働いています。浮力の理解は、船や潜水艦の設計、気球や飛行船の運行など、さまざまな分野で重要です。
剛体
剛体
剛体は、形状や大きさが変わらない理想的な物体のことです。例えば、硬い鉄の棒や木の板などがイメージしやすいでしょう。剛体は、力が加わっても変形せず、内部の相対位置も変わらないため、運動や力の分析が簡単になります。現実の物体は完全な剛体ではありませんが、剛体として扱うことで、力学の問題をシンプルに考えることができます。例えば、橋の設計や建物の構造計算など、剛体の概念は多くの工学分野で応用されています。
力のモーメント
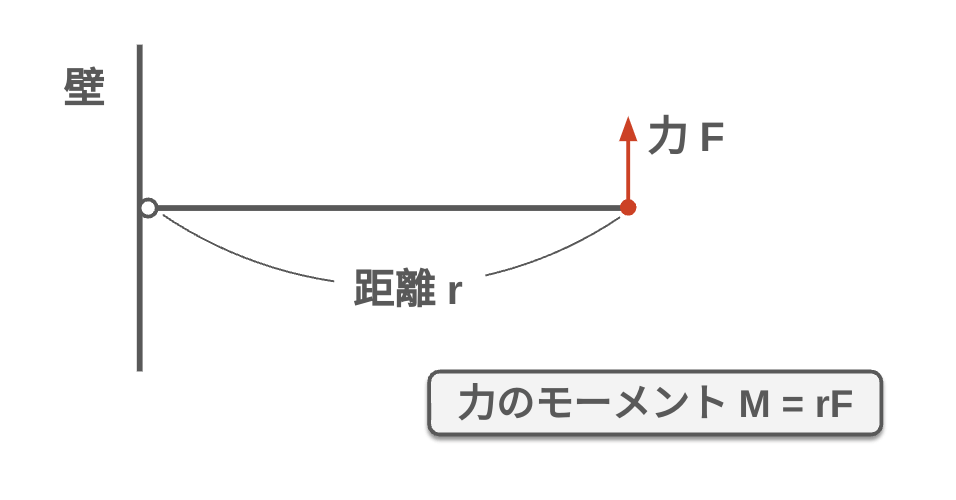
力のモーメントとは、力が物体を回転させる効果を表す量です。モーメントは、力の大きさと力の作用点から回転中心までの距離の積で求められます。例えば、ドアノブを押すとドアが回転するのは、ドアノブに加えた力がモーメントを生じさせるからです。モーメントの単位はニュートンメートル(Nm)です。モーメントの概念は、てこの原理や機械の設計など、回転運動を理解する上で重要です。
力のモーメント:\(M=rF\)
剛体に働く力のつり合い
剛体に働く力のつり合いは、物体が静止または等速直線運動を続けるために必要な条件です。剛体が静止するためには、物体に働く全ての力の合力がゼロであり、かつ全ての力のモーメントの合計がゼロである必要があります。例えば、シーソーが水平に保たれているとき、左右の力とモーメントがつり合っていることを示しています。この原理は、建築物の安定性や機械の設計などで重要な役割を果たします。
重心
重心は、物体の重さの中心を示す点です。重心は、物体がどのように配置されても常にその位置にあります。例えば、均一な密度の棒の重心は中央にありますが、片側が重い場合は重心がその方向に移動します。重心の位置を知ることで、物体の安定性やバランスを分析することができます。スポーツ選手やダンサーがバランスを取る際にも、重心の理解が重要です。重心は、建築や機械設計など多くの分野で応用されています。
変位・速度・加速度
変位・速度・加速度
変位は、物体の位置の変化を示す量で、始点から終点までの直線距離と方向を持ちます。速度は、単位時間あたりの変位の変化率を示し、速さと方向を持つベクトル量です。加速度は、単位時間あたりの速度の変化率を示し、運動の変化の度合いを表します。例えば、車が停止から出発して徐々に速度を上げるとき、その速度の変化が加速度です。これらの概念は、運動の詳細な分析や予測に不可欠です。
運動の合成・分解
運動の合成は、複数の運動を一つの運動にまとめることです。例えば、車が斜めに動くとき、その運動は水平運動と垂直運動に分けて考えられます。運動の分解は、一つの運動を複数の成分に分けることです。例えば、飛行機が風の影響を受けて進む方向を分析する際に用います。これにより、複雑な運動を簡単に理解し、予測することができます。運動の合成と分解は、物理現象の理解において基本的な手法です。
相対速度
相対速度は、ある物体の速度を他の物体から見た場合の速度です。例えば、電車内で歩いている人の速度は、電車の外から見ると電車の速度と歩く速度を合成したものになります。相対速度の概念は、動く物体同士の相対的な動きを理解するのに役立ちます。相対速度を正しく理解することで、移動中の物体間の距離や位置の変化を予測できます。この概念は、交通や航空の分野で重要です。
等加速度直線運動
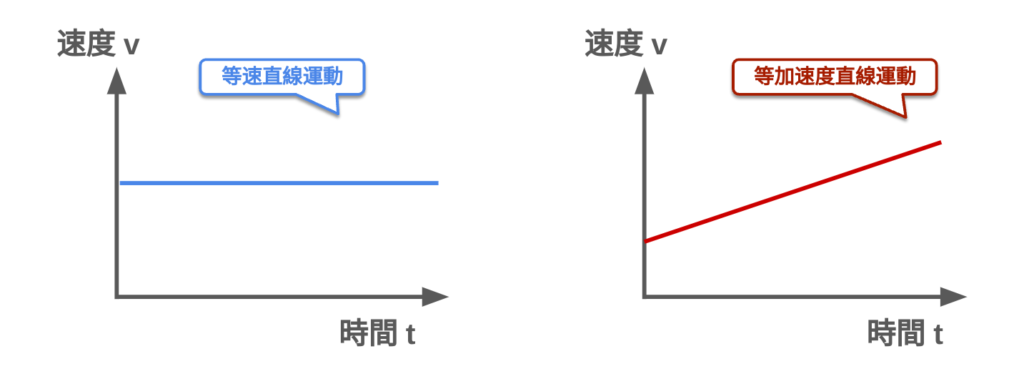
等加速度直線運動は、一定の加速度で直線的に運動する運動です。例えば、自由落下する物体は、重力によって等加速度直線運動をします。この運動では、速度が時間と共に一定の割合で変化し、変位は時間の二乗に比例して増加します。等加速度直線運動の基本的な公式は、運動の予測や分析に役立ちます。この概念は、車の加速やブレーキ、自由落下など、日常的な現象を理解するために重要です。
落体の運動
自由落下運動
自由落下運動は、重力のみが働く状況で物体が落下する運動です。例えば、リンゴが木から落ちるとき、その運動は自由落下運動です。自由落下運動では、物体は一定の加速度(9.8 m/s²)で加速し、速度は時間と共に増加します。この運動は、空気抵抗が無視できる場合に正確にモデル化できます。自由落下の原理は、物理学の基本法則であり、物体の運動を理解するための重要な概念です。
鉛直投射
鉛直投射は、物体を鉛直方向に投げ上げる運動です。例えば、ボールを真上に投げると、その運動は鉛直投射になります。この運動では、物体は上昇しながら減速し、最高点で速度がゼロになります。その後、物体は加速しながら落下します。鉛直投射の運動は、初速度や重力加速度を考慮して計算できます。この運動の理解は、物体の運動軌道や時間を予測するのに役立ちます。
水平投射
水平投射は、物体を水平に投げ出す運動です。例えば、テーブルの端からボールを水平に転がすと、その運動は水平投射になります。この運動では、物体は水平に一定速度で進みながら、重力によって垂直方向に加速します。その結果、物体は放物線を描いて落下します。水平投射の運動は、水平速度と垂直加速度を考慮して計算できます。この運動の理解は、物体の飛距離や落下時間を予測するのに役立ちます。
斜方投射
斜方投射は、物体を斜め方向に投げ出す運動です。例えば、バスケットボールをゴールに向かって投げるとき、その運動は斜方投射になります。この運動では、物体は斜めに一定の初速度で進み、重力の影響で放物線を描きます。斜方投射の運動は、初速度、投射角度、重力加速度を考慮して計算できます。この運動の理解は、物体の軌道や到達距離を予測するのに役立ちます。
まとめ
本記事では高校物理の「力学」の定義や法則の①をまとめました。
力学は、物体の動きや力の働きを研究する物理学の分野です。物体の運動やその原因となる力を理解することで、自然界の様々な現象を説明できます。例えば、リンゴが木から落ちる現象や車が走るときの加速など、日常生活で見られる多くの動きは力学で説明できます。ニュートンの運動の法則が力学の基本であり、これにより物体の運動状態がどう変わるかを予測できます。力学は、工学や建築、スポーツなど、多くの分野で応用されており、私たちの生活に密接に関わっています。
本記事で少しでも高校物理の「力学」の学習に役立てていたら幸いです。
その他の高校物理まとめは下記の黄色い枠のリンクから↓



