半導体キャリア密度の理解は,回路やセンサ開発などの応用の上でも重要です.本記事ではまず,半導体のキャリア密度の計算に必要な,状態密度関数とフェルミ・ディラック分布関数の解説します.その後,真性半導体と不純物半導体のキャリアについて,温度との関係などを交えながら説明していきます.
キャリアとは
キャリアは,移動できる電子 (伝導電子)と正孔 (ホール)のことです.半導体では電子・正孔が移動することで,電流が流れます.(詳しくはこちら)
半導体のキャリア密度
半導体のキャリア密度の理解は半導体の理解・応用の点で重要です.以下で説明しますが,キャリア密度は状態密度関数とフェルミ・ディラック分布関数から求めることができます.
状態密度関数とフェルミ・ディラック分布関数
伝導電子 (移動できる電子)の密度は ①「伝導帯に電子が存在できる席の数」,②「席に電子が埋まっている確率」から求めることができます.状態密度関数は ①の「伝導帯に電子が存在できる席の数」を示す関数です.フェルミ・ディラック分布関数は ②の「席に電子が埋まっている確率」を示す関数です.同様に,移動できる正孔の密度も状態密度関数とフェルミ・ディラック分布関数から求められます.
以下に,それぞれの式を示します (波形は次節で示してます).
伝導帯の電子の状態密度関数
\(g_C(E)=4\pi(\frac{2m_n^*}{h^2})^{\frac{3}{2}}(E-E_C)^{\frac{1}{2}}\)
価電子帯の正孔の状態密度関数
\(g_V(E)=4\pi(\frac{2m_p^*}{h^2})^{\frac{3}{2}}(E_V-E)^{\frac{1}{2}}\)
電子のフェルミ・ディラック分布関数
\(f_n(E)=\frac{1}{1+\exp(\frac{E-E_F}{kT})}\)
正孔のフェルミ・ディラック分布関数
\(f_p(E)=1-f_n(E)=\frac{1}{1+\exp(\frac{E_F-E}{kT})}\)
\(h\):プランク定数
\(m_n^*\):電子の有効質量
\(m_p^*\):正孔の有効質量
\(E_C\):伝導帯の下端のエネルギー
\(E_V\):価電子帯の上端のエネルギー
\(k\):ボルツマン定数
\(T\):絶対温度
正孔のフェルミ・ディラック分布関数\(f_p(E)\)は電子の存在しない確率と等しいです.次で,これら状態密度関数とフェルミ・ディラック分布関数を使って,キャリア密度を求めていきます.
真性半導体のキャリア密度
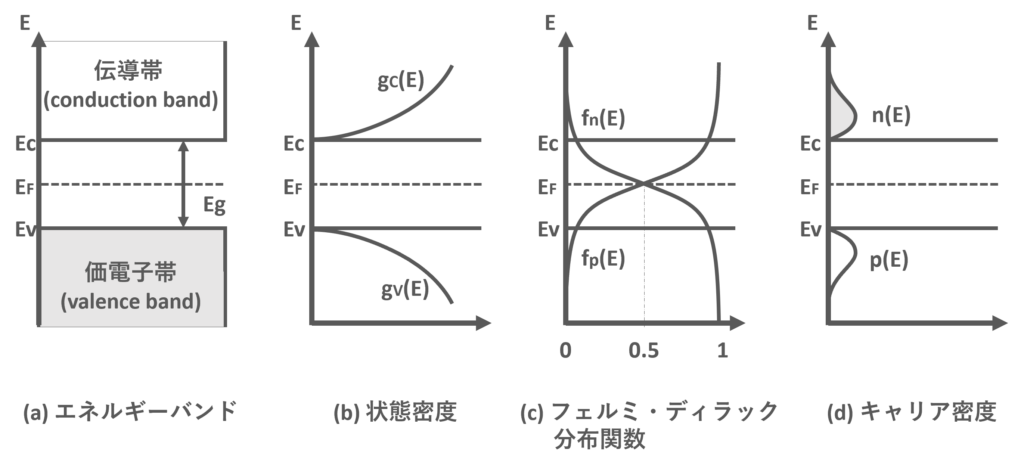
図1に真性半導体の(a)エネルギーバンド ,(b)状態密度 ,(c)フェルミ・ディラック分布関数 ,(d)キャリア密度を示します.
\(E_F\)はフェルミ・ディラック分布関数が0.5になるときのエネルギーです.キャリア密度は状態密度関数とフェルミ・ディラック分布関数の積で求めます.エネルギー\(E\)のときの電子数は\(n(E)\),正孔の数は\(p(E)\)となります.詳細な計算は省きますが電子密度\(n\),正孔密度\(p\)は以下のようになります.
\(n=\displaystyle \int_{E_C}^{\infty}g_C(E)f_n(E)dE=N_C\exp(\frac{E_F-E_C}{kT})\)
\(p=\displaystyle \int_{-\infty}^{E_V}g_V(E)f_p(E)dE=N_V\exp(\frac{E_V-E_F}{kT})\)
\(N_C=2(\frac{2\pi m_n^*kT}{h^2})^{\frac{3}{2}}\):伝導帯の実行状態密度
\(N_V=2(\frac{2\pi m_p^*kT}{h^2})^{\frac{3}{2}}\):価電子帯の実行状態密度
真性キャリア密度
真性半導体のキャリアは熱的に電子と正孔が対で励起されるため,電子密度\(n\)と正孔密度\(p\)は等しくなります.真性半導体のキャリア密度を真性キャリア密度\(n_i\)といい,以下の式のようになります.後ほど説明しますが,不純物半導体の電子密度\(n\)と正孔密度\(p\)の積の根も\(n_i\)になります.
\(n_i=\sqrt{np}\)
温度の変化によるキャリア密度の変化
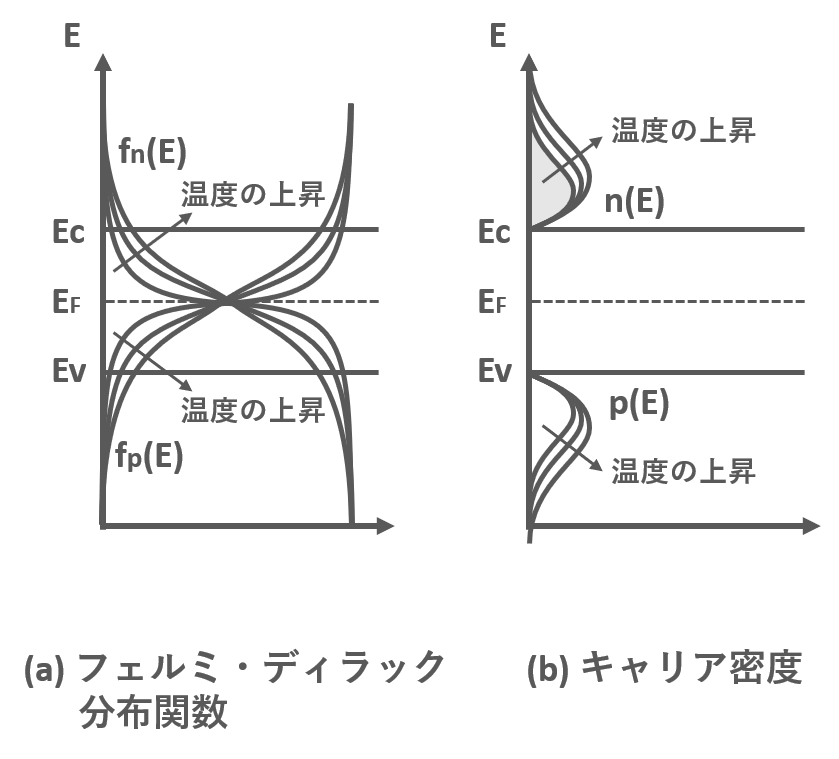
真性半導体の場合は熱のエネルギーで電子と正孔が励起されます.上で示したキャリア密度の式からもわかるように,半導体の温度が上がるの連れてキャリア密度も高くなります.温度の上昇により,キャリア密度が高くなる様子を図2に示します.温度が上昇すると図2 (a)のようにフェルミ・ディラック分布関数が変化していき,キャリア密度も増加します.
不純物半導体のキャリア密度
不純物半導体は不純物を添付した半導体です.キャリアが電子の半導体はn型半導体,キャリアが正孔の半導体がp型半導体です.図3にn型半導体のキャリア密度,図4にp型半導体のキャリア密度の様子を示します.
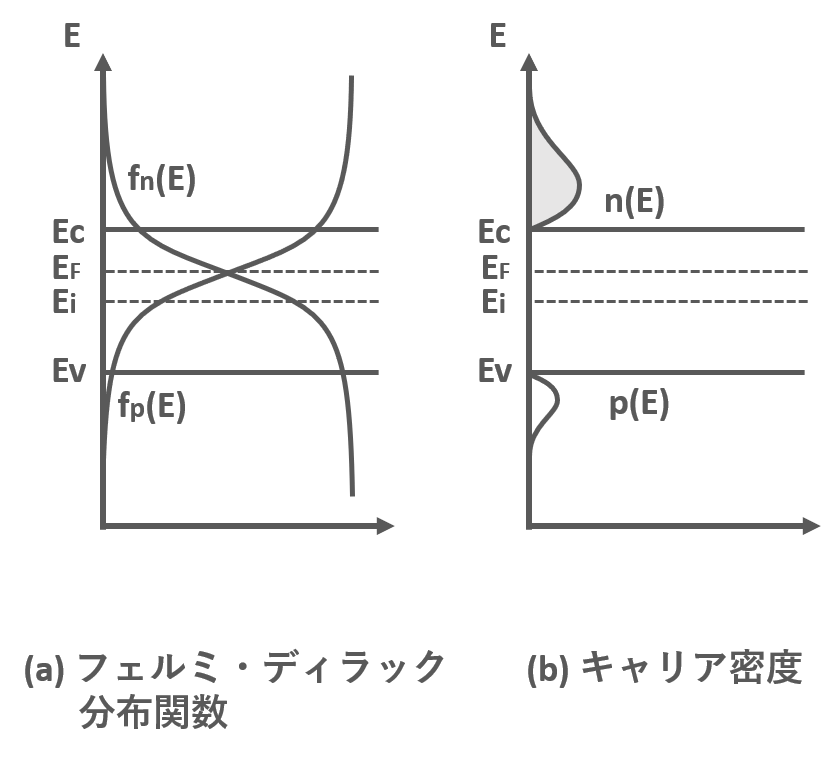
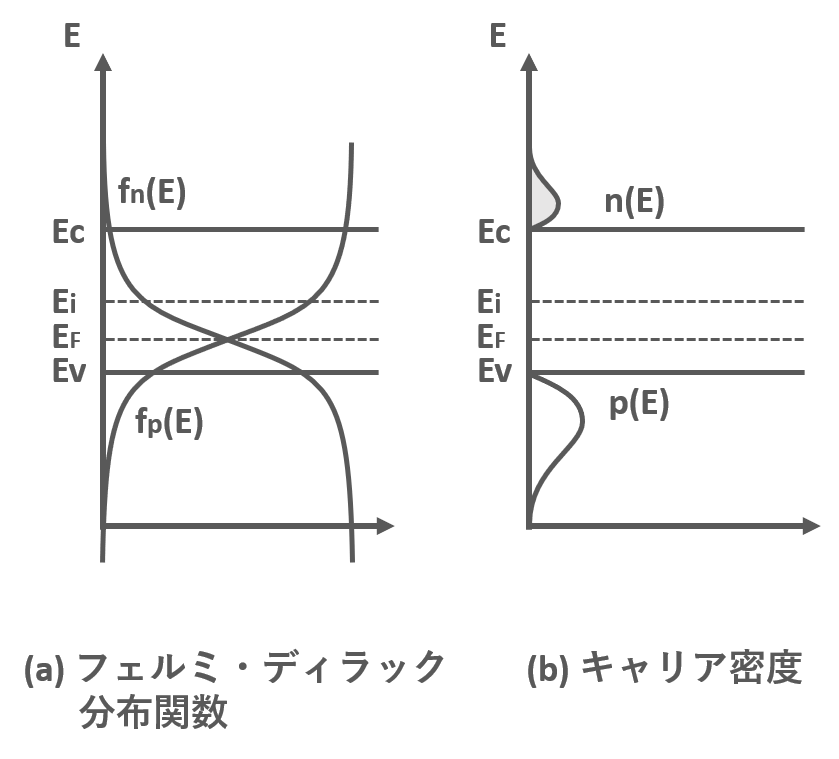
n型半導体では電子のキャリア密度が正孔のキャリア密度より高く,p型半導体では正孔のキャリア密度が電子のキャリア密度より高いです.より多いキャリアを多数キャリア,少ないキャリアを少数キャリアといいます.不純物半導体のキャリア密度は以下の式のように表されます.
\(n=n_i\exp(\frac{E_F-E_i}{kT})\)
\(p=n_i\exp(\frac{E_i-E_F}{kT})\)
\(E_i\)は真性フェルミ準位といい,真性半導体では\(E_i=E_F=\frac{E_C-E_V}{2}\)の関係があります.不純物半導体では不純物を注入することでフェルミ準位\(E_F\)が変化して,キャリア密度も変化します.計算するとわかりますが不純物半導体の場合でも\(np=n_i^2\)の関係が成り立ちます.これは半導体に不純物を注入することで,片方のキャリアが増える代わりにもう片方のキャリアは減ることを示しています.また不純物を注入しても通常は総電荷は0になるため,n型半導体では\(qp-qn+qN_d=0\) (\(N_d\):ドナー密度),p型半導体では\(qp-qn-qN_a=0\) (\(N_a\):アクセプタ密度)の関係があります.
まとめ
- 状態密度関数:伝導帯に電子,価電子帯の正孔が存在できる席の数を示す関数
- フェルミ・ディラック分布関数:その席に電子,正孔が埋まっている確率
- 真性キャリア密度:\(n_i=\sqrt{np}\)
- 不純物半導体のキャリア密度:\(n=n_i\exp(\frac{E_F-E_i}{kT})\),\(p=n_i\exp(\frac{E_i-E_F}{kT})\)



