導体
導体とは
導体とは導体は金属などの電気を通しやすい物体のこと.
静電しゃへい
静電しゃへい導体で作られた空間内では,外部の電界を遮る.これを静電しゃへい (シールド)という.
電界内にある導体は静電誘導によって外部との電界を打ち消しあうため,導体内では外部の電界の影響を受けないためである.
測定器などで外部の電界を影響を抑えることに用いられる.
静電容量
コンデンサ
コンデンサ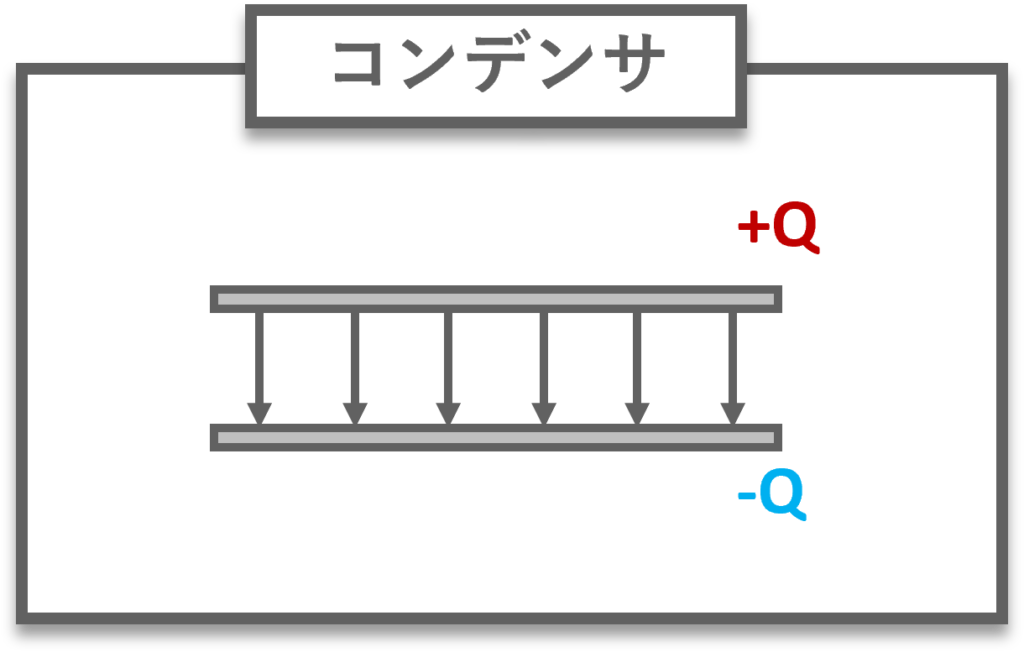
2つの導体にそれぞれ電荷+Qと電荷-Qを与えて近づけると,電気力線は一つからもう一つへと終端される.このように電荷を蓄えることができる素子をコンデンサ (蓄電器,キャパシタ (capacitor))という.
静電容量
静電容量2つの導体にそれぞれ電荷+Qと電荷-Qを与え,2つの導体の電位差がVのとき,\(Q=CV\)が成り立つ.Cは静電容量 (キャパシタンス (capacitance))といい,単位はF (ファラド (farad))である.静電容量は電荷をどれだけ蓄えられるかを示す.
平行導体板の静電容量
平行導体板の静電容量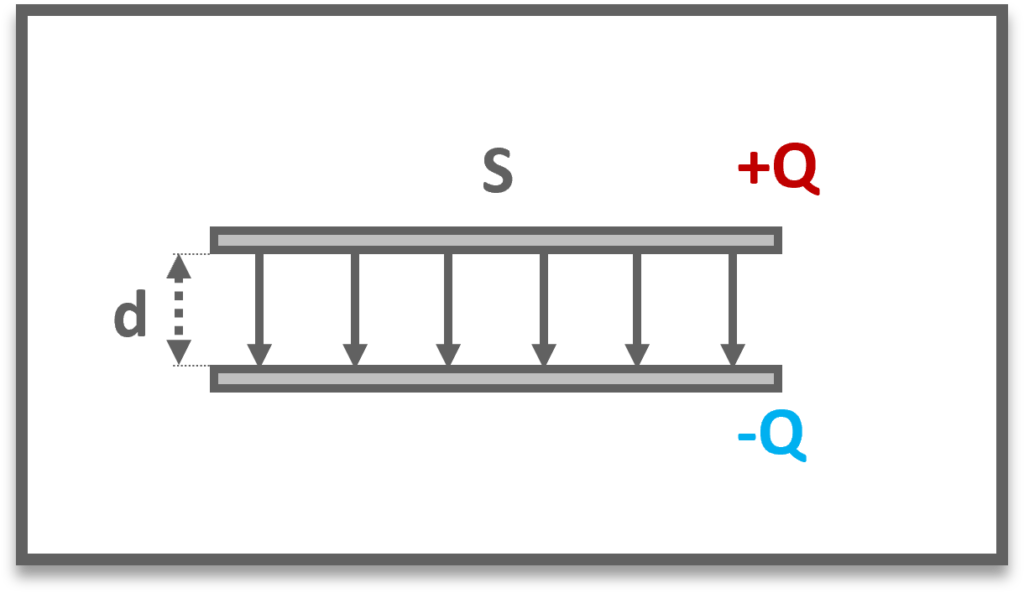
平行導体板の静電容量は以下の通りである.
$$C=\frac{Q}{V}=\frac{\epsilon_0S}{d}$$
コンデンサの並列接続
コンデンサの並列接続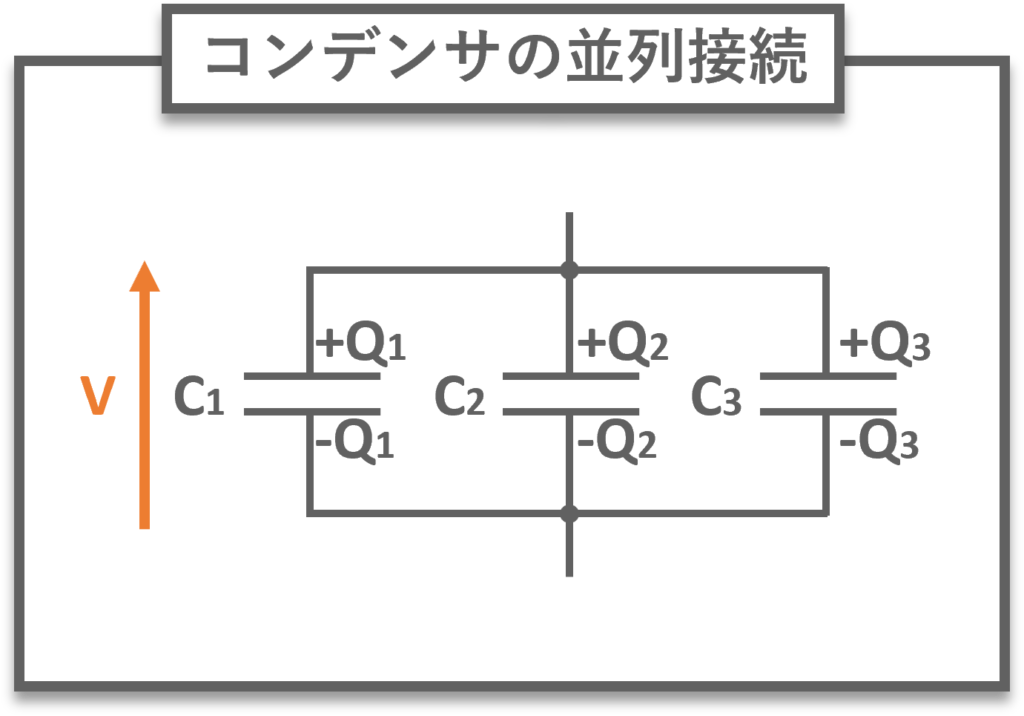
コンデンサの並列接続の合成容量\(C_{合成}\)は以下のようになります.
\(Q_1=C_1V,\)
\(Q_2=C_2V,\)
\(Q_3=C_3V,\)
\(Q_{合成}=Q_1+Q_2+Q_3\)より
\(C_{合成}=\frac{Q_{合成}}{V}\)
\( =C_1+C_2+C_3\)
コンデンサの直列接続
コンデンサの直列接続
コンデンサの直列接続の合成容量\(C_{合成}\)は以下のようになります.
\(V_1=\frac{Q}{C_1},\)
\(V_2=\frac{Q}{C_2},\)
\(V_3=\frac{Q}{C_3}\)
⇒\(V=V_1+V_2+V_3\)
⇒\(C_{合成}=\frac{Q}{V}\)
⇒\(\frac{1}{C_{合成}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\)
コンデンサのエネルギー
コンデンサのエネルギーコンデンサのエネルギーは以下の通りです.
$$W=\frac{1}{2}\frac{Q^2}{C}=\frac{1}{2}QV=\frac{1}{2}CV^2 [J]$$


