“余弦定理”の公式とその証明です!
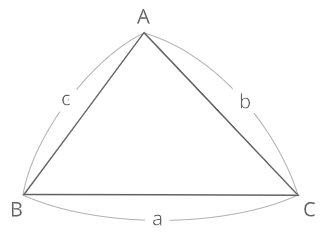
余弦定理
公式
余弦定理\(・a^{2}=b^{2}+c^{2}-2bccosA\)
\(・b^{2}=c^{2}+a^{2}-2cacosB\)
\(・c^{2}=a^{2}+b^{2}-2abcosC\)
証明
三平方の定理による証明
証明
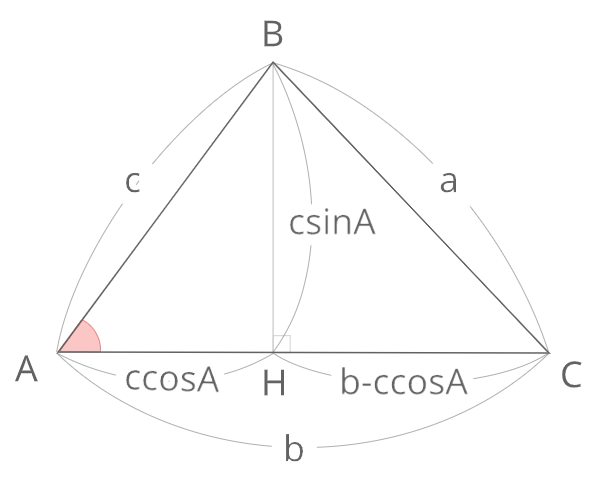
∠BHCが直角になるようにHをとると
・BH=csinA
・HC=b-ccosA
となる。
三平方の定理より
\(BC^2=BH^2+HC^2\)
\(a^2=(csinA)^2+(b-ccosA)^2\)
\(=c^2sin^2A+b^2-2bccosA+c^2cos^2A\)
\(=b^2+c^2(sin^2A+cos^2A)-2bccosA\)
\(=b^2+c^2-2bccosA\)
よって
\(a^{2}=b^{2}+c^{2}-2bccosA\)
まとめ
余弦定理は大変便利で使える場面も多いと思うのでしっかりと使えるようにしておいたほうがいいと思います.



