MOSFETのチャネル長変調効果について解説していきます.MOSFETの基礎と動作を理解に役立ててください.
チャネル長変調効果
チャネル長変調効果とは
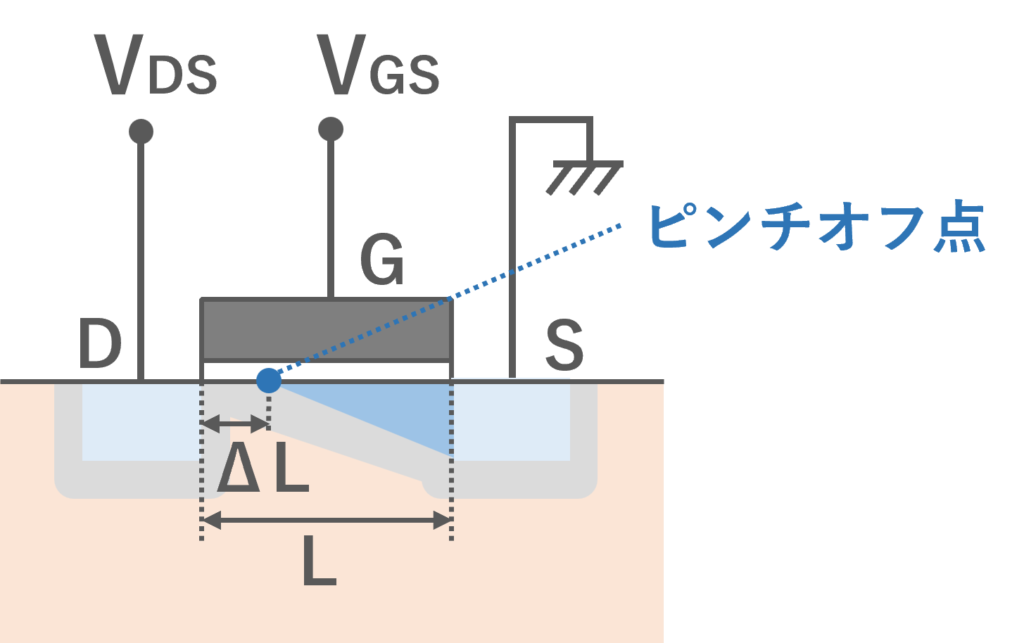
MOSFETの飽和領域では,ドレイン電圧\(V_{DS}\)によってドレイン近くの反転層がなくなり (ピンチオフ点),ドレイン電圧を増やしてもドレイン電流が増えなくなると説明しました.しかし実際は下図のように,飽和してからさらにドレイン電圧を高くすると,反転層がなくなる点 (ピンチオフ点)がソース側に移動していくことでドレイン電流も少しずつ増えていきます.このチャネル (ソースからドレイン,あるいはピンチオフ点までの距離)が変化する効果をチャネル長変調効果といいます.
このチャネル長変調効果を考慮した場合としない場合のドレイン電圧-ドレイン電流のグラフは下図のようになります.その下にそれぞれの式も示しています.次節ではチャネル長変調効果を考慮した場合の式の導出をしていきます (考慮しない場合はこちらで求めています).
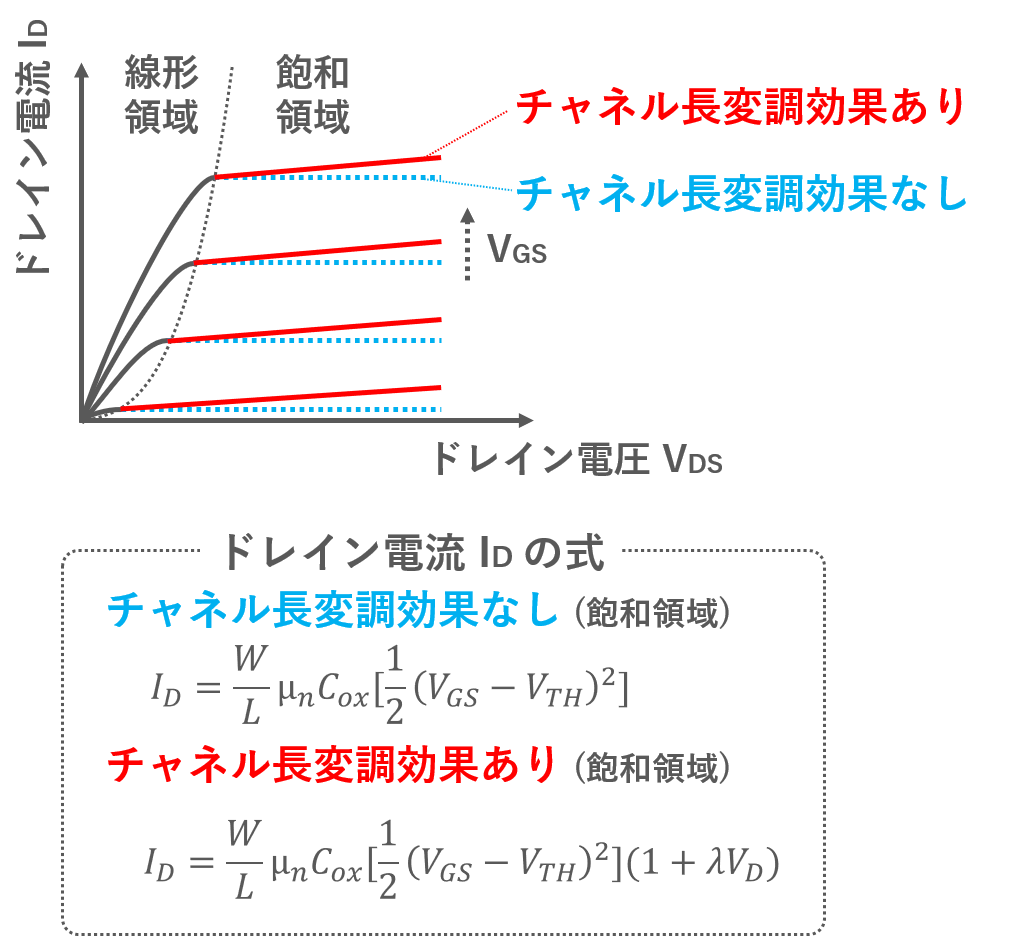
- \(\mu_n\):電子の移動度
- \(C_{ox}\):ゲート容量
- \(W\):ゲート幅
- \(L\):ゲート長
- \(V_{TH}\):しきい値電圧
- \(V_{GS}\):ゲート電圧
- \(V_{DS}\):ドレイン電圧
式の導出
チャネル長変調効果を考慮した場合のnMOSの飽和領域でのドレイン電流の導出をしていきます.下図にこのときの図を示しています.

飽和領域ではドレイン電圧\(V_{DS}\)を上げていくにつれ,チャネル長変調効果によりゲート長が\(\Delta L\)短くなります.そのためチャネル長変調効果なしの場合のnMOSの飽和領域での式から,\(L→L-\Delta L\)とすればチャネル長変調効果ありの場合の式が求められます.
チャネル長変調効果なしの場合の式は以下の通りです.(チャネル長変調効果なしの式導出はこちら).
\(I_{D}=\frac{1}{2}\frac{W}{L}\mu_nC_{ox}(V_{GS}-V_{TH})^2 (チャネル長変調効果なし)\)
この式の\(L→L-\Delta L\)とすると,チャネル長変調効果ありの式は以下のように計算できます.
\(I_D=\frac{W}{L-\Delta L}\mu_nC_{ox}[\frac{1}{2}(V_{GS}-V_{TH})^2]\)
\( = \frac{1+\frac{\Delta L}{L}}{1-\frac{\Delta L^2}{L^2}}\frac{W}{L}\mu_nC_{ox}[\frac{1}{2}(V_{GS}-V_{TH})^2] \)
\(L^2≫\Delta L^2\)より,\(\frac{\Delta L^2}{L^2} ≒ 0\)とできるため
\( ≒ \frac{W}{L}\mu_nC_{ox}[\frac{1}{2}(V_{GS}-V_{TH})^2](1+\frac{\Delta L}{L})\)
\(\Delta L\)は\(V_{DS}\)に依存するため,\(\frac{\Delta L}{L}=\frac{cV_D}{L}=\lambda V_D (cは定数)\)とできるため
\(I_D=\frac{W}{L}\mu_nC_{ox}[\frac{1}{2}(V_{GS}-V_{TH})^2](1+\lambda V_D)\)
となります.また式よりLが小さいと\(\lambda\)が大きくなり,よりチャネル長変調効果の影響が大きくなることがわかります.
まとめ
ドレイン電流 (飽和領域,チャネル長変調効果なし)
\(I_D=\frac{W}{L}\mu_nC_{ox}[\frac{1}{2}(V_{GS}-V_{TH})^2]\)
ドレイン電流 (飽和領域,チャネル長変調効果あり)
\(I_D=\frac{W}{L}\mu_nC_{ox}[\frac{1}{2}(V_{GS}-V_{TH})^2](1+\lambda V_D)\)



