高校物理の「熱力学」の定義・法則などをまとめました。勉強に役立ててもらえれば幸いです。
熱
熱力学とは
熱力学とは熱力学とは、熱と仕事、およびエネルギーの変換を扱う物理の分野である。
熱運動
熱運動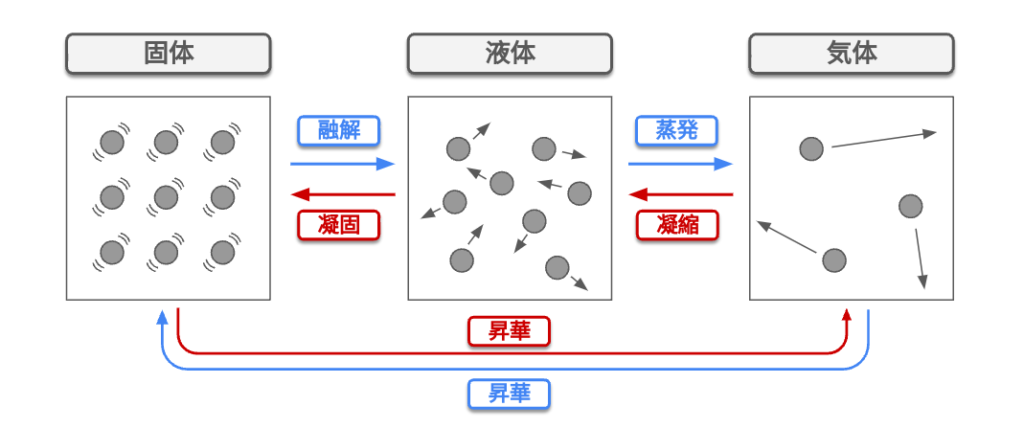
熱運動とは、物質を構成する原子や分子が絶えず不規則に運動している現象である。温度が高いほど、分子の運動は激しくなる。
温度
温度温度とは、物体の熱の状態を表す量で、分子の熱運動の激しさの目安となる物理量である。温度が高いほど、分子の平均運動エネルギーは大きい。
【セルシウス温度】
・単位:℃
・水の凝固点を0度、沸点を100度とした温度
【ケルビン温度】
・単位:K (ケルビン)
・物質は-273℃まで温度を下げると熱運動が停止して、これよりも温度は低くならない。この温度を絶対零度と呼び、絶対温度を基準とした温度がケルビン温度。ケルビン温度=セルシウス温度 + 273
熱平衡・熱・熱量
熱平衡・熱・熱量コップに入った水に熱した鉄球を入れて時間が経過すると鉄球と水の温度は等しくなり、温度は変化しなくなる。この状態を「熱平衡」と呼ぶ。このときに温度の高い物体 (鉄球)から温度の低い物体 (水)に移ったエネルギーを「熱」と呼び、移動した熱の量を「熱量」と呼ぶ。
熱容量・比熱
熱容量・比熱使われるある物体の温度を1 [K]上昇させるのに必要なエネルギーを「熱容量」という。記号はQで単位は[J/K (ジュール/ケルビン)]が使われる。
物体は物質の種類によって熱しやすさ・冷めやすさが異なるように、熱容量は物質によって異なる。単位質量あたりの熱容量を「比熱 (比熱容量)」という。記号はc、単位は[J/g・K (ジュール/グラム・ケルビン)]が使われる。
鉄は水よりも熱しやすく、冷めやすいが、これは鉄の比熱が水よりも小さいためである。
熱量の保存
熱量の保存コップに入った水に熱した鉄球を入れると鉄球の熱が水に移る。このときに鉄球と水の熱がコップやコップの外には移動しないと仮定すると、鉄球から水に熱が移る前後では熱量の総量は変わらない。これを「熱量の保存」という。
熱の仕事当量・ジュールの実験
熱の仕事当量・ジュールの実験熱の仕事当量とは、熱と仕事が同じエネルギーの形であり、一定の割合で互いに変換できることを表す関係である。
ジュールの実験により、仕事 と発生する熱量 は比例し、1カロリーは約 に相当することが示された。
気体
物質の三態
物質の三態
氷を熱すると水になり、水をさらに熱すると水蒸気になる。
このように、物質は一般的に固体・液体・気体の3つの状態があり、これを「物質の三態」という。
「融点」:固体が液体になる温度 (液体が固体になる温度)
「沸点」:液体が気体になる温度 (気体が液体になる温度)
固体・液体・気体とは
固体・液体・気体とは
固体:物質の原子などの粒子が互いに結合している状態
液体:粒子間の結びつきは弱いが、一定の距離で熱運動をしている状態
気体:粒子が互いに結びついておらず、様々な速度で自由に飛び回っている状態
気体の法則
気体の圧力
気体の圧力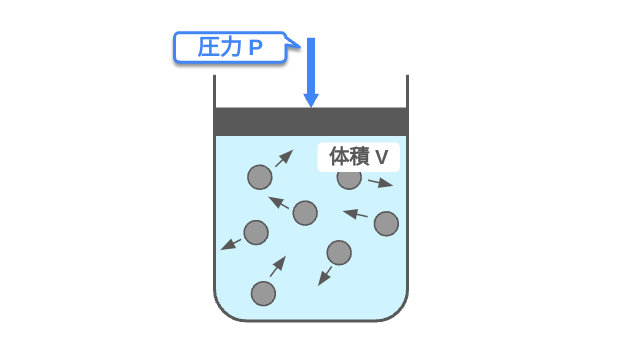
気体の圧力とは、気体分子が容器の壁に衝突して単位面積あたりに及ぼす力である。分子運動が激しいほど、圧力は大きくなる。
圧力pは\(p=F (力)/S (面積)\)の関係があり、単位はPa (パスカル) = N/m\(^2\)である。
ボイル・シャルルの法則
ボイル・シャルルの法則一定質量の気体は下式のような「ボイル・シャルルの法則」が成り立つ。
$$pV/T=(一定)$$
\(p\)は圧力、\(V\)は体積、\(T\)は温度である。実際には分子の大きさや分子間になどを考慮するとこの法則が少しずれるが、分子の大きさなどの効果を無視してボイル・シャルルの法則に正確に従う気体を「理想気体」と呼ぶ。
理想気体の状態方程式
理想気体の状態方程式理想気体では下式の「状態方程式」が成り立つ
$$pV=nRT$$
\(p\)は圧力、\(V\)は体積、\(n\)は物質量、\(R\)は気体定数、\(T\)は温度である。この状態方程式は気体が理想気体のときに成り立つものだが、常温・常圧あたりでは理想気体として状態方程式で扱うことができる。
気体分子の運動
気体分子の運動分子数\(N\)個、質量\(m\)、気体分子の平均速度\(v\)、体積\(V\)の気体の圧力は\(p\)は下記のようになる
$$p=\frac{Nmv}{3V}$$
気体分子の運動エネルギー
気体分子の運動エネルギー気体分子の平均運動エネルギーは下式の関係がある
$$1/2mv^2=3/2kT$$
\(m\)は質量、\(v\)は分子の平均速度、\(k\)はボルツマン定数、\(T\)は温度。
内部エネルギー
内部エネルギー分子は熱運動による熱エネルギーや分子間で互いに力を与える位置エネルギーを持つ。これらは物質が持つ隠れたエネルギーで「内部エネルギー」という。
単原子分子の理想気体では分子間の力は無視できるため、このときの内部エネルギー (単原子分子理想気体の内部エネルギー)は下記のようになる。
【単原子分子理想気体の内部エネルギー】
$$U=3/2nRT$$
熱力学第1法則
熱力学第1法則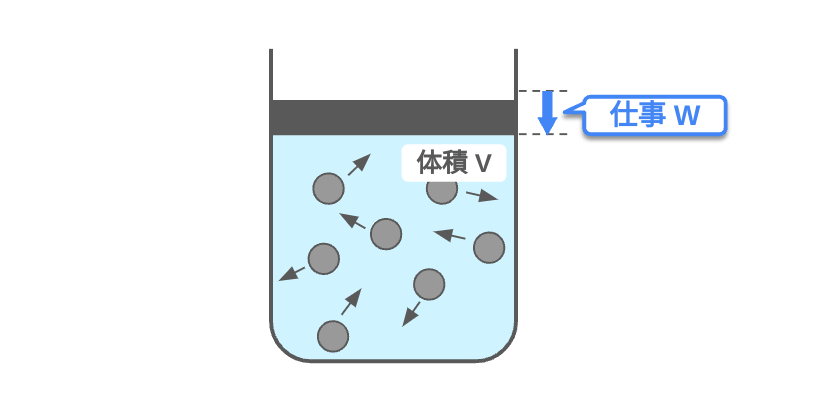
下式のように、物体に与えた熱量\(Q\)[J]と物体にした仕事 \(W\) [J]の和は物体の内部エネルギーの変化 \(\Delta U\) [J]に等しく、これを「熱力学第一法則」という。
$$\Delta U=Q+W$$
これはある系でのエネルギーが保存されることを示します。
気体の状態変化
気体の状態変化【定積変化】
体積が一定での状態の変化を「定積変化」という。このとき、体積は変化しないため仕事\(W\)は0であるため、熱力学第一法則より
内部エネルギーの変化\(\Delta U\) = 物体に与えた熱量 \(Q\)
が成り立つ。
【定圧変化】
圧力が一定での状態の変化を「定圧変化」という。このとき、圧力 \(p\)は変化しないため仕事\(W\)は\(p \Delta V\)であるため、熱力学第一法則より
\(\Delta U = Q + p \Delta V\)
が成り立つ。
モル比熱
モル比熱物質1molの温度を1 [K]上昇させるための熱量を「モル比熱」という。
不可逆変化・熱機構
不可逆変化
不可逆変化高温に熱した鉄球は周りの温度が低ければ熱を失って温度が下がるが、鉄球を熱したり外部の温度を高くするなどの外部から何かしらの操作をしなければ鉄球が周りから熱を吸収して再び高温になることはない。
このような外部から何かしらの操作をしなければ元の状態に戻ることができない変化を「不可逆変化」という。また、この法則を「熱力学第二法則」という。
熱機関
熱機関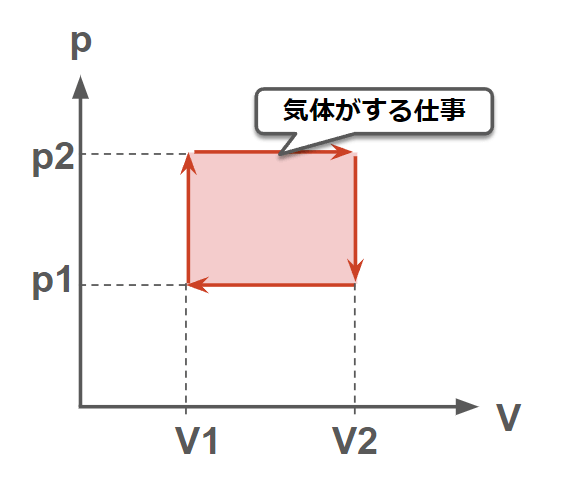
エンジンのように燃料を燃焼して得られる熱を仕事に変換する装置を「熱機関」という。
熱機関では図のように燃焼を利用して圧力と体積をサイクルさせて熱を仕事に変換させる。図のようなサイクルでは赤枠で囲まれた面積が気体がした仕事となる。
熱効率
熱効率熱機関では熱量のすべてが仕事には変換されない。この熱量の内で仕事に利用された割合を「熱効率」という。熱効率 \(e\)は下記の式が成り立つ。
$$e=\frac{W}{Q_1}=\frac{Q_1-Q_2}{Q_1}$$
\(W\)は熱機関がする仕事、\(Q_1\)は高温の物体から吸収する熱量、\(Q_2\)は低温の物体へ放出熱量である。熱効率は \(e<1\)となる。
永久機関
永久機関「永久機関」は一度動かすと外部からエネルギーを与えなくても仕事をし続ける装置の概念である。しかし、永久機関は熱力学の法則より、不可能であることが分かっている。
まとめ
本記事では高校物理の「熱力学」の定義や法則をまとめました。
熱力学の理解はエネルギー変換やエネルギーの流れを理解し、日常生活や産業に役立てるために不可欠です。熱力学はエンジンや冷蔵庫の原理から、天候の変化や自然現象まで様々な現象を説明します。また、エネルギーの効率的な利用や持続可能なエネルギー源の開発にも繋がります。
本記事で少しでも高校物理の「熱力学」の学習に役立てていたら幸いです。
その他の高校物理まとめは下記の黄色い枠のリンクから↓



