【高校数学】”sinθ/θの極限”の公式とその証明

証明

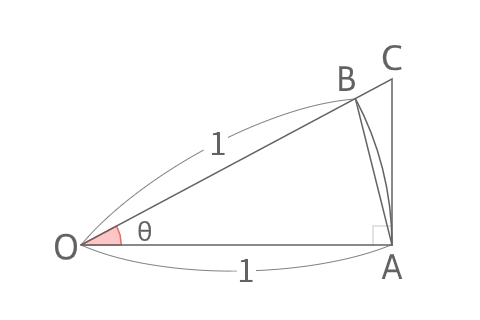
\(0<θ<\frac{π}{2}\)のとき
上の図より\(△OAB\)、\(\stackrel \frown{AB}\)とする扇形\(OAB、△OAC\)の面積はそれぞれ
\(\frac{1}{2}sinθ<\frac{1}{2}θ<\frac{1}{2}tanθ\)
⇒ \(sinθ<θ<tanθ\)
となる。さらにそれぞれを\(sinθ\)で割ると
\(1<\frac{θ}{sinθ}<\frac{1}{cosθ}\)
また\(θ→0\)のとき\(\displaystyle \lim_{θ→0}\frac{1}{cosθ}=1\)であるため挟みうちの原理より
\(\displaystyle \lim_{θ→0}\frac{θ}{sinθ}=1\)
つまり\(0<θ<\frac{π}{2}\)のとき\( \displaystyle \lim_{θ→0}\frac{sinθ}{θ}=1\)となる。
\(\frac{-π}{2}<θ<0\)のときも同様に\( \displaystyle \lim_{θ→0}\frac{sinθ}{θ}=1\)となる。
よって
\( \displaystyle \lim_{θ→0}\frac{sinθ}{θ}=1\)