【高校数学】”双曲線の性質”の公式とその証明

“双曲線の性質”の公式とその証明です！

双曲線の性質

公式

双曲線\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1　(a>0, b>0)\)において
　・焦点　\(F(\sqrt{a^2+b^2}, 0)、　F'(-\sqrt{a^2+b^2}, 0)\)
　・双曲線上の点Pで　　|PF-PF’|=2a

証明

証明

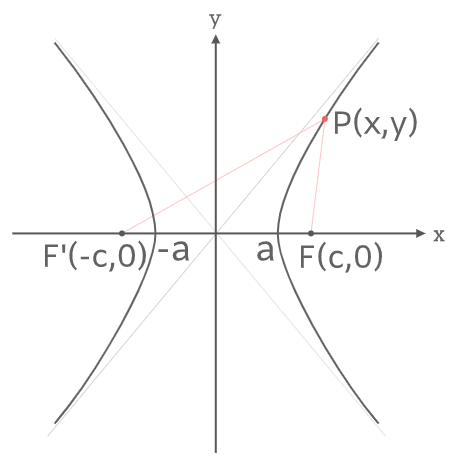
まず双曲線の定義は焦点を\(F(c,0)、F'(-c,0)\)、楕円上の点を\(P(x,y)\)としたときに、
\(|PF-PF’|=2a\)となる。
よって上の図より
\(|\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}|=2a\)
⇒ \(\sqrt{(x-c)^2+y^2}=±2a+\sqrt{(x+c)^2+y^2}\)
両辺を２乗して整理すると
\(a^2+xc=±\sqrt{(x+c)^2+y^2}\)
さらに両辺を２乗して整理すると
\((c^2-a^2)x^2-a^2y^2=a^2(c^2-a^2)\)
\(c^2-a^2=b^2\)とすると　　　　　①
\(b^2x^2-a^2y^2=a^2b^2\)
⇒ \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)

また①より
\(c^2=a^2+b^2\)
⇒ \(c=±\sqrt{a^2+b^2}\)
a>0,b>0より
焦点は\(F(\sqrt{a^2-b^2}, 0)、F'(-\sqrt{a^2-b^2}, 0)\)

よって
双曲線\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1　(a>0, b>0)\)において
　・焦点　\(F(\sqrt{a^2+b^2}, 0)、　F'(-\sqrt{a^2+b^2}, 0)\)
　・双曲線上の点Pで　　|PF-PF’|=2a

数３の公式一覧とその証明