“累乗の和”の公式とその証明です!
累乗の和
公式
累乗の和\(・\displaystyle\sum_{k=1}^nc=nc\)
\(・\displaystyle\sum_{k=1}^nk=\frac{1}{2}n(n+1)\)
\(・\displaystyle\sum_{k=1}^nk^{2}=\frac{1}{6}n(n+1)(2n+1)\)
\(・\displaystyle\sum_{k=1}^nk^{3}=\{\frac{1}{2}n(n+1)\}^2\)
証明
\(\displaystyle\sum_{k=1}^nk=\frac{1}{2}n(n+1)\)の証明
証明
\(\displaystyle\sum_{k=1}^nk=S\)とすると
\(S=1+2+3+\)\(…+(n-2)+(n-1)+n ①\)
これを逆順で表すと
\(S=n+(n-1)+(n-2)+\)\(…+3+2+1 ②\)
①、②を足し合わせると
\(2S\)
\(=(n+1)+(n+1)+(n+1)+\)\(…+(n+1)+(n+1)+(n+1)\)
\(=n(n+1)\)
よって
\(S=\frac{1}{2}n(n+1)\)
つまり
\(\displaystyle\sum_{k=1}^nk=\frac{1}{2}n(n+1)\)
\(\displaystyle\sum_{k=1}^nk^{2}=\frac{1}{6}n(n+1)(2n+1)\)の証明
証明
以下の恒等式を用いる
\(・k^3-(k-1)^3=3k^2-3k+1\)
この恒等式を1~nまでを足し合わせると
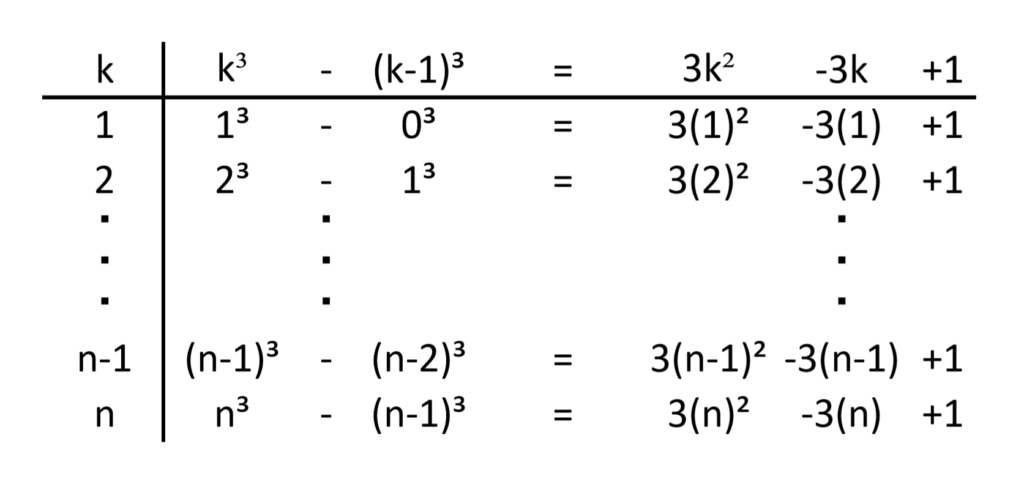
左辺でそれぞれ打ち消しあい
\(n^3= \displaystyle\sum_{k=1}^n3k^{2}-\displaystyle\sum_{k=1}^n3k+n\)
となり、順番を変えると
\(3\displaystyle\sum_{k=1}^nk^{2}=n^3+\displaystyle\sum_{k=1}^n3k-n\)
\(・\displaystyle\sum_{k=1}^nk=\frac{1}{2}n(n+1)\)より
\(3\displaystyle\sum_{k=1}^nk^{2}\)
\(=n^3+\frac{3}{2}n(n+1)-n\)
\(=\frac{n}{2}(n^2+3n+1)\)
\(=\frac{n}{2}(2n+1)(n+1)\)
よって
\(\displaystyle\sum_{k=1}^nk^{2}=\frac{1}{6}n(n+1)(2n+1)\)
\(\displaystyle\sum_{k=1}^nk^{3}=\{\frac{1}{2}n(n+1)\}^2\)の証明
証明
以下の恒等式を用いる
\(・k^4-(k-1)^4=4k^3-6k^2+4k-1\)
この恒等式を上の証明のように足し合わせると
\(n^4=\displaystyle\sum_{k=1}^n4k^{3}-\displaystyle\sum_{k=1}^n6k^{2}+\displaystyle\sum_{k=1}^n4k-n\)
となり、順番を変えると
\(\displaystyle\sum_{k=1}^n4k^{3}=n^4+\displaystyle\sum_{k=1}^n6k^{2}-\displaystyle\sum_{k=1}^n4k+n\)
\(・\displaystyle\sum_{k=1}^nk=\frac{1}{2}n(n+1)\)
\(・\displaystyle\sum_{k=1}^nk^{2}=\frac{1}{6}n(n+1)(2n+1)\)より
\(\displaystyle\sum_{k=1}^n4k^{3}\)
\(=n^4+\frac{6}{6}n(2n+1)(n+1)-\frac{4}{2}n(n+1)+n\)
\(=n^4+2n^3+n^2\)
\(=n^2(n^2+2n+1)\)
\(=n^2(n+1)^2\)
よって
\(\displaystyle\sum_{k=1}^nk^{3}=\{\frac{1}{2}n(n+1)\}^2\)



