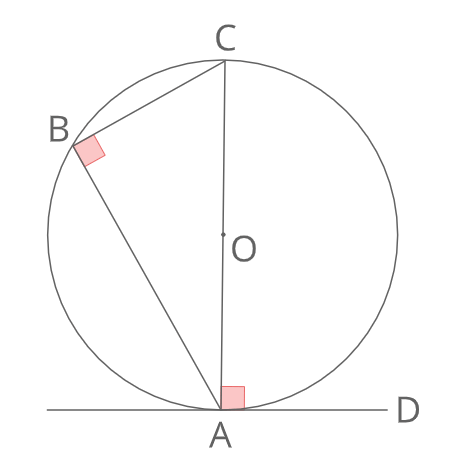
“接弦定理”の公式とその証明です!
接弦定理
公式
接弦定理円の接線とその接点を通る弦とがなす角は、その角内にある孤に対する円周角に等しい 。
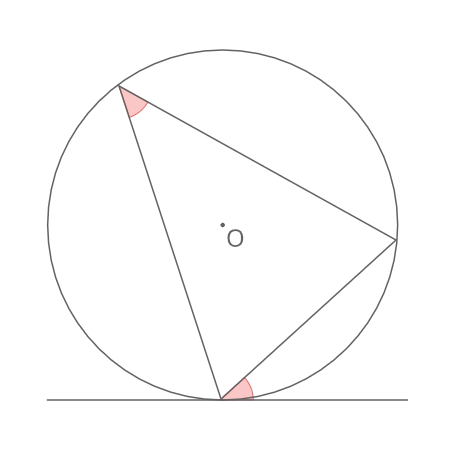
証明
以下では鋭角のとき、直角のとき、鈍角のときの3つの場合でそれぞれ証明する。
接弦定理(鋭角のとき)の証明
証明
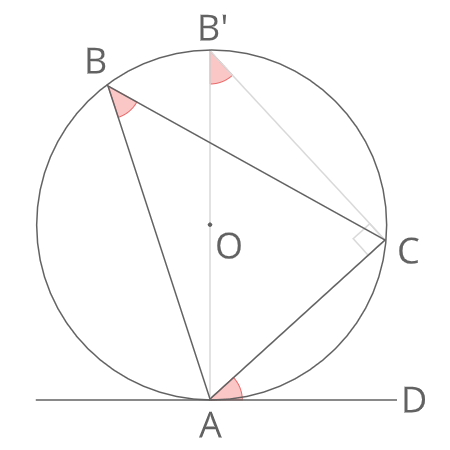
∠DACが鋭角のとき
点Aと円の中心Oの延長線上と円の交点をB’とする。
円周角の定理より
∠B=∠B’ ①
また
∠ACB’=90°
よって
∠B’AC+ 90°+∠B’
=∠B’AC+ 90°+∠CAD
⇒ ∠B’=∠DAC ②
①、②より
∠B=∠DAC
よって鋭角のとき
円の接線とその接点を通る弦とがなす角は、その角内にある孤に対する円周角に等しい 。
接弦定理(直角のとき)の証明
接弦定理(鈍角のとき)の証明
証明
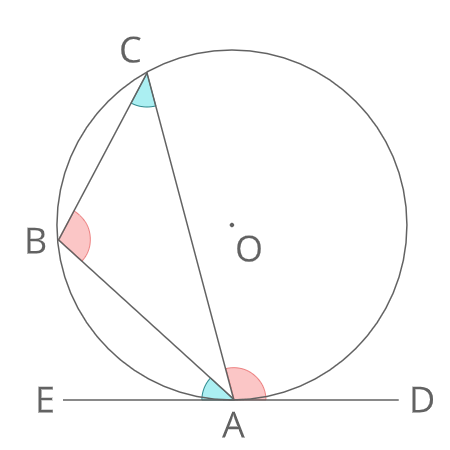
∠DACが鈍角のとき
すでに証明したように鋭角のときの接弦定理より
∠C=∠EAB
∠C+∠BAC+∠B
=180°
=∠EAB+∠BAC+∠DAC
=∠C+∠BAC+∠DAC
⇒∠B=∠DAC
よって鈍角のとき
円の接線とその接点を通る弦とがなす角は、その角内にある孤に対する円周角に等しい 。
問題
Q
三角形ABCが円Oに内接するとき,図の∠ACBを求めよ
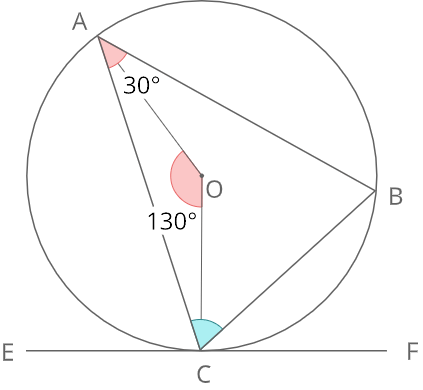
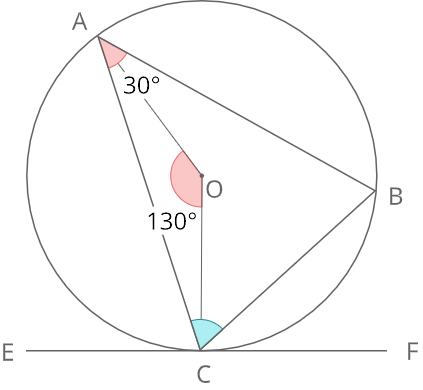
A
接弦定理より
\(∠BCF=∠BAC=30°\) ①
円周角の定理より
\(∠ABC=\frac{∠AOC}{2}=65°\)
接弦定理より
\(∠ACE=∠ABC=65°\) ②
①,②より
\(∠ACB=180°-∠ABC-∠ACE\)
\(=180°-30°-65°\)
\(85°\)となります.
まとめ
三角形が円に内接している場合に接弦定理が使えることもあるので使えるようにしておきましょう.