“円周角の定理”の公式とその証明です!
円周角の定理
公式
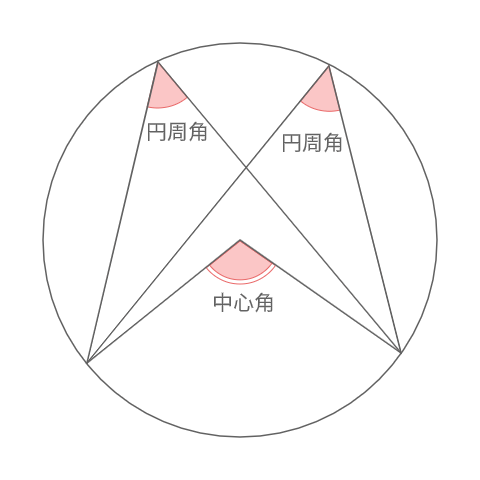
円周角の定理・同じ弧に対する円周角の大きさは中心角の大きさの半分
・同じ弧に対する円周角は等しい
証明
以下では中心を通るとき、中心を含むとき、中心が外のときの3つの場合でそれぞれ証明する。
中心を通るときの証明
証明
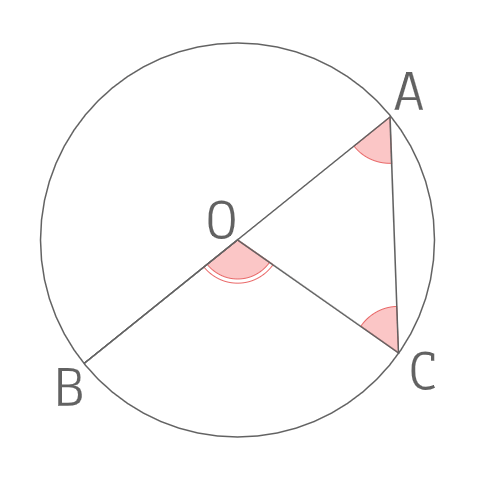
上の図よりOAとOCは共に円Oの半径であるため△OACは二等辺三角形となり
\(∠OAC=∠OCA\) ①
となる。また∠BOCは∠AOCの外角となるため
\(∠BOC=∠OAC+∠OCA\)
①より
\(∠BOC=2∠OAC\)
よって
円周角を作る1辺が円の中心を通るとき、
同じ弧に対する円周角の大きさは中心角の大きさの半分
中心を含むときの証明
証明
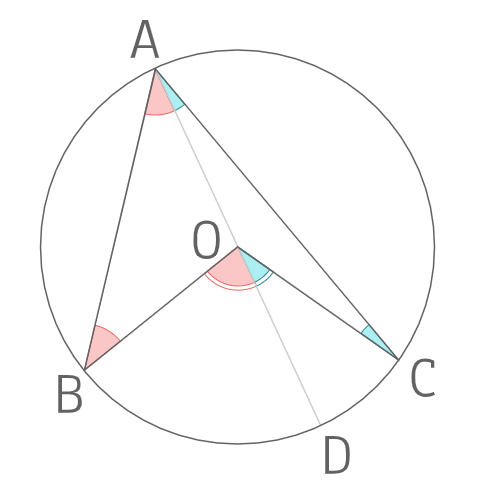
上の図のように円の中心を通る線ADを加え、中心を通るときと同様に
円周角∠OACにおいて
\(∠OAC=∠OCA\) ①
となる。また∠DOCは∠AOCの外角となるため
\(∠DOC=∠OAC+∠OCA\)
①より
\(∠DOC=2∠OAC\) ②
となる。また円周角∠OABにおいても同様に
\(∠OAB=∠OBA\) ③
となる。また∠DOBは∠AOBの外角となるため
\(∠DOB=∠OAB+∠OBA\)
③より
\(∠DOB=2∠OAB\) ④
②、④より
\(∠DOC+∠DOB =2∠OAC+2∠OAB\)
⇒ \(∠BOC=2∠BAC\)
よって
円周角内に円の中心を含むとき、
同じ弧に対する円周角の大きさは中心角の大きさの半分
中心が外のときの証明
証明
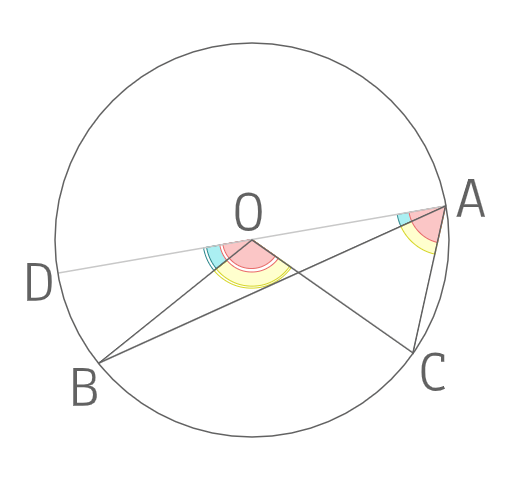
上の図のように円の中心を通る線ADを加え、中心を通るときと同様に
円周角∠OACにおいて
\(∠OAC=∠OCA\) ①
となる。また∠DOCは∠AOCの外角となるため
\(∠DOC=∠OAC+∠OCA\)
①より
\(∠DOC=2∠OAC\) ②
また円周角∠OABにおいても同様に
\(∠OAB=∠OBA\) ③
となる。また∠DOBは∠AOBの外角となるため
\(∠DOB=∠OAB+∠OBA\)
③より
\(∠DOB=2∠OAB\) ④
②、④より
\(∠DOC-∠DOB =2∠OAC-2∠OAB\)
⇒ \(∠BOC=2∠BAC\)
よって
円周角の外に円の中心があるとき、
同じ弧に対する円周角の大きさは中心角の大きさの半分
また以上の3つの場合の証明より同じ弧に対する円周角の大きさは常に中心角の大きさの半分であるため、同じ弧に対する円周角は等しい
問題
Q
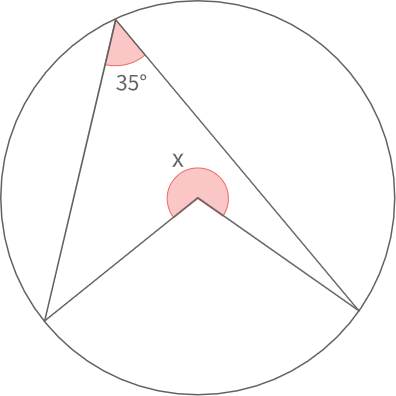
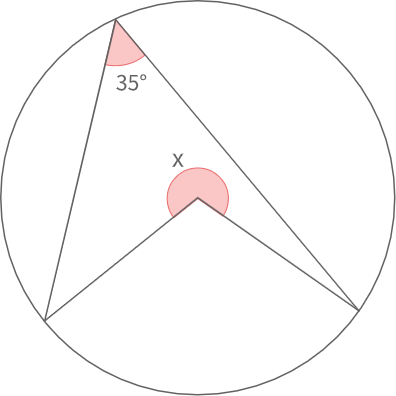
図の角度xを求めよ
A
円周角の定理より
\(x=360°-2×35°\)
\(=290°\)となります.
まとめ
円と三角形の組み合わせでよくでてくるので使えるようにしておきましょう.



