“外角の二等分線と比”の公式とその証明です!
外角の二等分線と比
公式
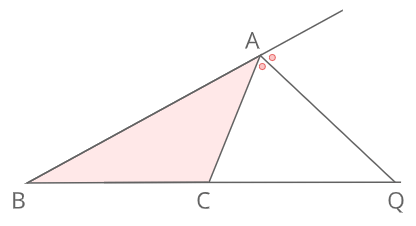
外角の二等分線と比点Aの外角の二等分線とBCの延長との交点をQとすると
\(BQ:QC=AB:AC\)
証明①
三角形の相似による証明
証明
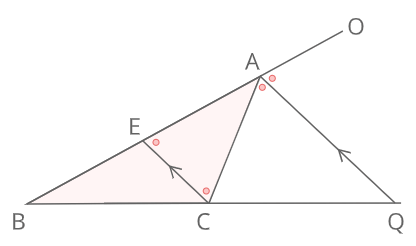
Cを通りAQに平行な線とABの交点をEとし、BAの先をOとする。
AQとECは平行であるため錯角と同位角より
∠AEC=∠ACE=∠CAQ=∠OAQ
よって△AECは二等辺三角形である。なので
AE=AC ①
また△EBC∽△ABQなので
BQ:QC=AB:AE ②
①、②より
BQ:QC=AB:AC
証明②
三角形の面積の比による証明
証明

底辺をBC、CQとすると高さが等しいため
BQ:QC=△ABQ:△ACQ ①
また\(∠QAC=\frac{1}{2}(180°-θ)=90°-\frac{θ}{2}\)より
\(△ABQ=AB×AQsin(90°+\frac{θ}{2})\)
\(AB×AQcos\frac{θ}{2}\) ②
\(△ACQ=AC×AQsin(90°-\frac{θ}{2})\)
\(AC×AQcos\frac{θ}{2}\) ③
①、②、③より
BQ:QC=AB:AC
問題
Q
点Aの外角の二等分線とBCの延長との交点をQのとき,図のxを求めよ
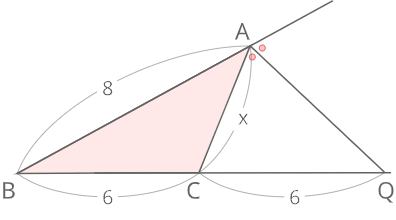
A
外角の二等分線と比により
\(12:6=8:x\)
⇒\(x=\frac{6\times 8}{12}\)
\(=4\)
よって
\(x=4\)となります.
まとめ
図の問題で三角形の外角が二等分線で分けられるときは外角の二等分線と比が使えるのでしっかり使えるようにしておきましょう.



