“三角関数 (三角比)の相互関係”の公式とその証明です!
三角関数 (三角比)の相互関係
公式
三角関数の相互関係 \(・sin^2θ+cos^2θ=1\)
\(・tanθ=\frac{sinθ}{cosθ}\)
\(・1+tan^2θ=\frac{1}{cos^2θ}\)
証明
\(sin^2θ+cos^2θ=1\)の証明
証明
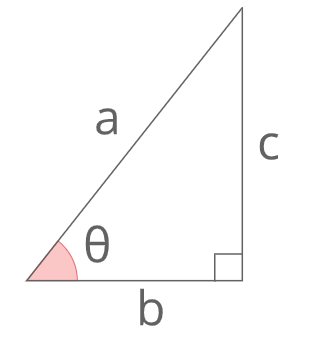
三角比の定義
\(sinθ=\frac{c}{a}\)
\(cosθ=\frac{b}{a}\)
より
\(sin^2θ+cos^2θ\)
\(=(\frac{c}{a})^2+(\frac{b}{a})^2 \)
\(=(\frac{1}{a^2})(c^2+b^2)\)
また三平方の定理より
\(=(\frac{1}{a^2})(a^2)\)
\(=1\)
よって
\(sin^2θ+cos^2θ=1\)
\(tanθ=\frac{sinθ}{cosθ}\)の証明
証明

三角比の定義より
\(sinθ=\frac{c}{a}\)
\(cosθ=\frac{b}{a}\)
\(tanθ=\frac{c}{b}\)
さらに
\(\frac{sinθ}{cosθ}\)
\(=\frac{c}{a}\frac{a}{b}\)
\(=\frac{c}{b}\)
\(=tanθ\)
よって
\(tanθ=\frac{sinθ}{cosθ}\)
\(1+tan^2θ=\frac{1}{cos^2θ}\)の証明
証明
\(sin^2θ+cos^2θ=1\)
の両辺を\(cos^2θ\)で割ると
\(\frac{sin^2θ}{cos^2θ}+1=\frac{1}{cos^2θ}\)
また\(tanθ=\frac{sinθ}{cosθ}\)より
\(tan^2θ+1=\frac{1}{cos^2θ}\)
よって
\(1+tan^2θ=\frac{1}{cos^2θ}\)
問題
Q
\(\frac{tan^2\theta}{1-cos^2\theta}\frac{cos^2\theta}{cos^2\theta+sin^2\theta}\)を求めよ.
A
\(\frac{tan^2\theta}{1-cos^2\theta}\frac{cos^2\theta}{cos^2\theta+sin^2\theta}\)
三角関数の相互作用より
\(=\frac{tan^2\theta}{1-cos^2\theta}\frac{cos^2\theta}{1}\)
\(=\frac{\frac{sin^2\theta}{cos^2\theta}}{1-cos^2\theta}\frac{cos^2\theta}{1}\)
\(=\frac{sin^2\theta}{1-cos^2\theta}\)
\(=\frac{sin^2\theta}{sin^2\theta}\)
\(=1\)
まとめ
三角関数の相互関係は三角関数の基礎中の基礎です.簡単な関係ですが自分で導き出せる必要があります.



