“三平方の定理”の公式とその証明です!
三平方の定理
公式
三平方の定理$$c^2=a^2+b^2$$
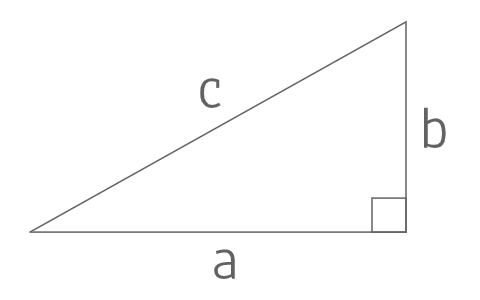
証明
図形による証明
証明
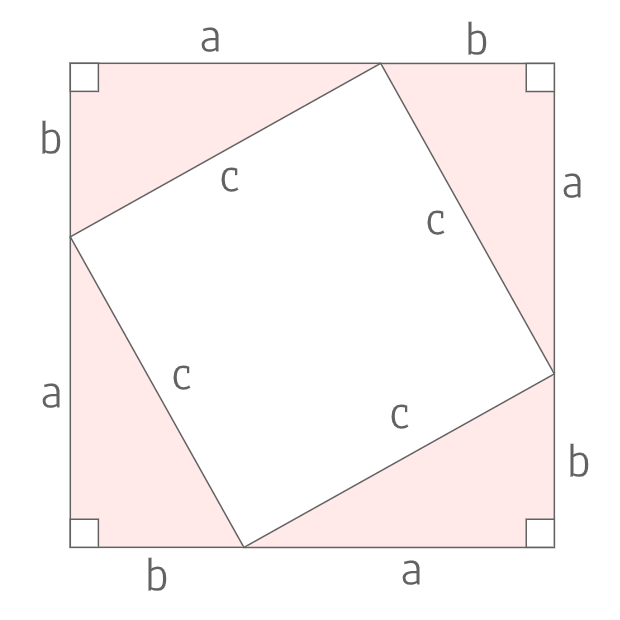
上の図より外側の四角形の面積は内側の四角形の面積と4つの三角形の面積の和に等しいため
\((a+b)^2=c^2+4×\frac{1}{2}ab\)
⇒ \(a^2+2ab+b^2=c^2+2ab\)
よって
\(c^2=a^2+b^2\)
問題
Q
図のxを求めよ
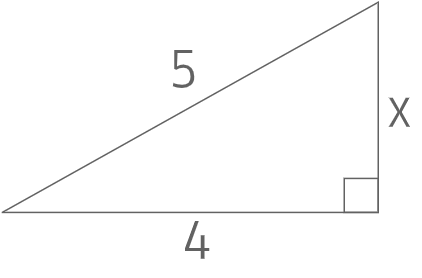
A
三平方の定理より
\(5^2=4^2+x^2\)
⇒\(x^2=5^2-4^2\)
\(=25-16\)
\(=9\)
よって
\(x=3\)
になります.
まとめ
三平方の定理(別名ピタゴラスの定理)は単純な公式ですが,使う場面も多いです.



