“扇形の弧の長さと面積”の公式とその証明です!
扇形の弧の長さと面積
公式
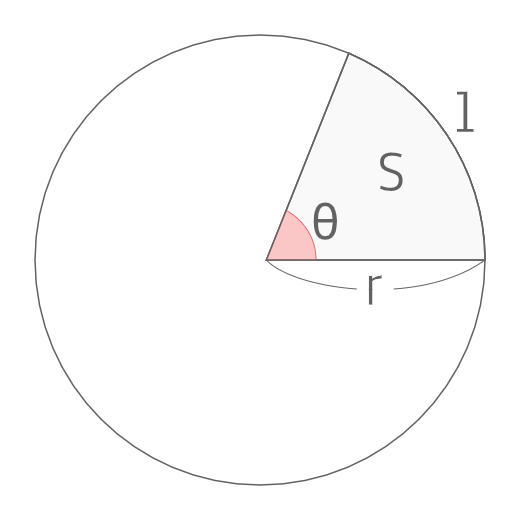
扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると
\(・l=rθ\)
\(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)
証明
比率による証明
証明
\((円周)=2πr\)より
\(θ:l=2π:2πr\)
⇒ \(l=\frac{2πrθ}{2π}\)
\(=rθ\)
よって
\(l=rθ\)
また
\((円の面積)=πr^2\)より
\(θ:S=2π:πr^2\)
⇒ \(S=\frac{πr^2θ}{2π}\)
\(=\frac{r^2θ}{2}\)
\(=\frac{1}{2}lr\)
よって
\(S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)



