“点と直線の距離”の公式とその証明です!
点と直線の距離
公式
点と直線の距離点\((x_1, y_1)\)と直線ax+by+c=0の距離dは
\(d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
証明
連立方程式による証明
証明
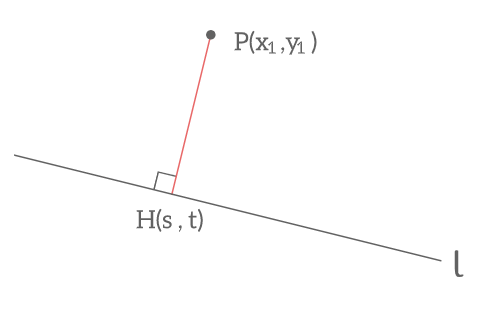
直線\(l : ax+by+c=0\)を変形すると
\(y=-\frac{a}{b}-\frac{c}{b}\)
よって直線\(l\)の傾きは\(-\frac{a}{b}\) ①
直線\(l\)上に垂直となるように点H(s,t)と置くとPHの傾きは
\(\frac{y_1-t}{x_1-s}\)となる ②
それぞれ垂直となる直線の傾きの積は\(-1\)となるため①、②より
\(-\frac{a}{b}\frac{y_1-t}{x_1-s}=-1\)
⇒ \(a(y_1-t)=b(x_1-s)\) ③
またH(s,t)は直線\(l\)上にあるため
\(as+bt+c=0\) ④
③、④の連立方程式より
\(s=\frac{-aby_1+b^2x_1-ac}{a^2+b^2}\) ⑤
点と直線lの距離dは
\(d=PH\)
\(=\sqrt{(s-x_1)^2+(t-y_1)^2}\)
\(=\frac{1}{a}\sqrt{a^2(s-x_1)^2+b^2(s-x_1)^2}\)
⑤を代入して計算すると
\(=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)
よって
点\((x_1, y_1)\)と直線ax+by+c=0の距離dは
\(d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}\)



