【高校数学】”円に内接する四角形”の公式とその証明

“円に内接する四角形”の公式とその証明です！

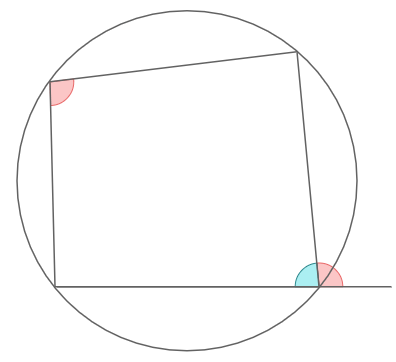
円に内接する四角形

公式

円に内接する四角形において
対角の和は180°

証明

円周角の定理による証明

証明

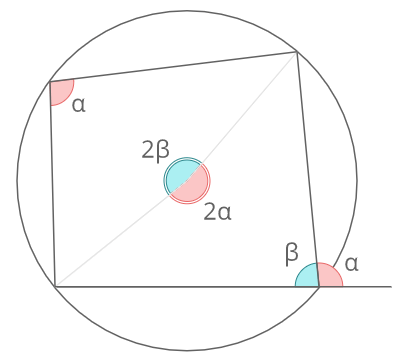
対角の関係にある角をそれぞれ∠α、∠βとすると円周角の定理により
∠2α＋∠2β=360°
⇒∠α＋∠β＝180°
よって
円に内接する四角形において対角の和は180°

問題

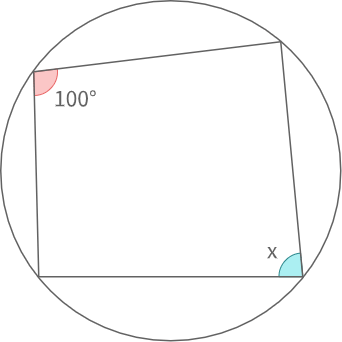
Q

図の角度xを求めよ

A

円に内接する四角形より
\(x=180°-100°\)
\(=80°\)となります．

まとめ

円に内接する四角形があるときには良く使われます．

まとめ記事に戻る

【高校数学】数Aの公式一覧とその証明まとめ！

高校数学の「数A」公式一覧とそれぞれ公式の証明をまとめました．大学受験などにご活用いただけたら幸いです．すでに高校を卒業した方でも，パズル感覚で公式の証明をするのも楽しいので，ぜひチャレンジしてみてください．各公式の右下にその公式の証明のリ

enggy.net