“チェバの定理”の公式とその証明です!
チェバの定理
公式
チェバの定理△ABCのBC、CA、AB上にそれぞれ点P、Q、Rがあるとき
\(\frac{PB}{CP}・\frac{RA}{BR}・\frac{QC}{AQ}=1\)
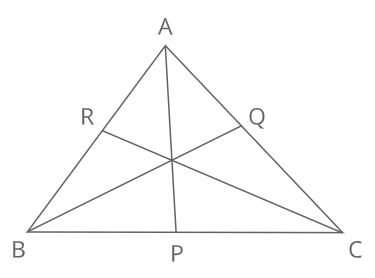
証明
面積比による証明
証明

上の図で、APを通る直線と点Bから垂直に交わる点をX、 APを通る直線と点Cから垂直に交わる点をYとする。
このときすべての角が等しくなるため△BXP∽△CYPとなる。
よって
PB:CP=BX:YC ①
△ABOと△CAOの底辺をAOとすると高さはそれぞれBXとYCとなる。
また①より
PB:CP= △ABO:△CAO
⇒\(\frac{PB}{CP}=\frac{△ABO}{△CAO}\) ②

同様に
RA:BR= △CAO:△BCO
⇒\(\frac{RA}{BR}=\frac{△CAO}{△BCO}\) ③
QC:AQ= △BCO:△ABO
⇒\(\frac{QC}{AQ}=\frac{△BCO}{△ABO}\) ④
を得る。
②、③、④の積より
\(\frac{PB}{CP}・\frac{RA}{BR}・\frac{QC}{AQ}= \frac{△ABO}{△CAO}・\frac{△BCO}{△ABO}・\frac{△CAO}{△BCO} =1\)
よって
\(\frac{PB}{CP}・\frac{RA}{BR}・\frac{QC}{AQ}=1\)
問題
Q
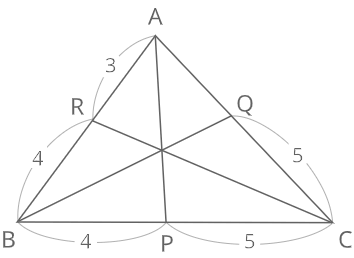
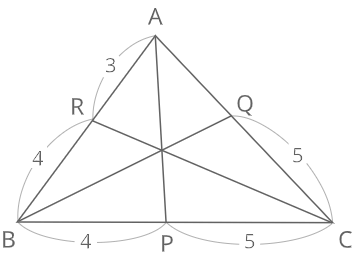
図のAQを求めよ
A
チェバの定理より
\(\frac{4}{5}・\frac{3}{4}・\frac{5}{AQ}=1\)
\(AQ=\frac{4}{5}・\frac{3}{4}・5\)
⇒\(AQ=3\)となります.
まとめ
複数の三角形等が交わっている場合はチェバの定理が使えることもあります.



